REVIEW OF MATH
2.1 Univariate calculus
Given two sets X and Y , a function is a rule that associates each member
of X with
exactly one member of Y . Intuitively, “y is a function of x” means that the
outcome y
depends on some x. For example, how happy you are might depend on how many
hours you spend playing softball each day; we would say that happiness (or
utility) is a
function of softball time. Mathematics provides convenient shorthand for writing
this compactly:
y = f (x)
In these cases, x is called the independent variable and y the
dependent
variable. That is, we can pick any value of x we want to stick into the
function, but
we can’t really pick what value y takes on—that depends on x.
When f is a function from X into Y , the set X is called the domain of
the function
and Y is called the range. The domain is the set of permissible values to
stick into
the function (if your earnings are some function of the number of hours you work
each day, then the domain of “number of hours per day” is from 0 to 24), and the
value that the function takes must be somewhere within the range. Most functions
used are real-valued functions: functions whose ranges are the set of
real
numbers. The domain is usually also a subset of the real numbers, but there’s no
reason that it has to be. Your happiness could be a function of something
abstract
and unquantifiable, like the flavor of tea you drink.
In economics, the amount of a good x demanded is a function of a person’s wealth
and the price of that good. In other words,
x = x( p, w)
This is called a demand function. Sometimes the same letter will be used
to
denote the function as the dependent variable.
Sometimes we will deal with inverse functions: that is, there is a
function that
associated each element of Y with an element of X. Usually the inverse of a
function
f is denoted by f -1 .
y = f (x) is equivalent to : x = f -1 (y) .
You can think of it this way: the function f tells you the output y you get from
the
input x; the inverse function f -1 tells you the input x necessary to
get output y.
The demand function tells us how much people want to buy at a certain price.
(Let’s
forget about wealth for now.) If a business knows this, it might ask the
question,
“given that we would like to get consumers to buy x units, what price should we
charge?” The business would simply find the inverse demand function:
x = x( p) is equivalent to: p = x-1 (x( p)) = p(x) .
In economics, we often use the term marginal to capture the effect of a
small
change in one thing on something else (like the marginal utility of consumption,
or
the marginal product of labor). This is akin to the mathematical concept of the
derivative of f at a point x:
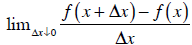
(Interpretation: the change in the function f from x to x
+ Δx , per unit of Δx , when
Δx gets as small as possible.) The derivative of f might be denoted by f' (x)
or,
when y = f (x) , by dy /dx . You’ll probably become familiar with these:
Utility function: U =U(c)
Marginal utility of consumption: dU /dc or U' (c)
Revenue function: R = p ·Y = p · F(L)
Marginal revenue product of labor: p · dF /dL or p · F' (L)
The derivative can also be interpreted as the slope of a line tangent to the
function at
that point. Think back to diagrams of total cost and marginal cost curves.
At this point, the most important to know is how to take a derivative.
Calculating the derivative of a function using the proper definition can be
very
tedious. In most cases, simple calculus rules simply it. The most important of
these
is the power rule :

Because you can often break down functions ( like
polynomials ) into several terms of
this form, you can take most derivatives easily using this. Here are some other
rules
to follow for taking derivatives:
| Addition rule: | 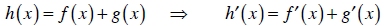 |
| Product rule: | 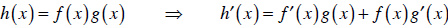 |
| Quotient rule: | 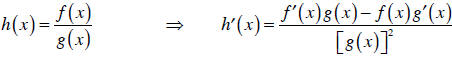 |
| Chain rule: |  |
| Inverse rule: | 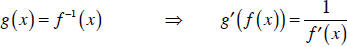 |
(The quotient rule and the inverse rule require that the
term in the denominator is
not zero , obviously.) The function h in the chain rule is called a composite
function; that is, h is not directly a function of x, but it is a
function f o f g(x) . If
that sounds confusing, think of this example: your utility is not actually a
function of
prices. However, prices do affect how much you can afford to buy, and that
affects
your utility. During this semester, you will see an individual’s indirect
utility
function. This is the composite function I just described:
V ( p, w) =U(x( p, w))
This is the value of having wealth w when facing prices p. It is simply the
utility you
get from your optimal demand x( p,w) at these prices with this wealth.
The inverse rule is also very useful for getting information from inverse
functions.
For example, a consequence of utility maximization is an equation like “the
marginal
utility of consuming some good equals the marginal cost (that is, price) of that
good”:
U' (x) = λ p
( λ is some constant, the multiplier from the utility maximization
problem—ignore it
for now.) This gives us an inverse demand function for x very easily:
U' (x) = λ p
What if we want to know how x changes when p changes? In other words, what is
the derivative of the demand function, dx /dp ? (Or what about the price
elasticity of
x? We would need to know dx /dp for that.) The inverse demand function gives us
the opposite of dx /dp :
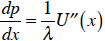
However, we can use the inverse rule to get what we want:
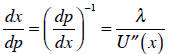
And that tells us how the optimal bundle will change when
the price changes. (The
idea is that the change in x resulting from a change in p depends on the
curvature of
the utility function.) As for point elasticity, the familiar “percent change in
this with
respect to a percent change in that” takes the form of:
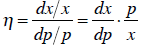
We found what dx /dp is. Using this and the original
optimality condition, we find
this formula for elasticity :
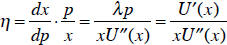
(The last term here might be familiar as relative risk
aversion, if you’ve taken
some advanced microeconomics).
As a final important note, some interesting f (x) have x as an exponent
or take the
logarithm of x. Two functions that show up frequently are exponential
e and the
natural logarithm ln . Remember these rules for exponents and logarithms:
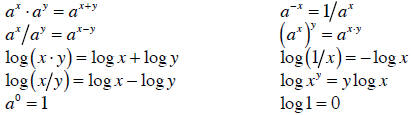
The power rule makes it easy to take the derivatives of
most functions. However,
these “interesting” functions—like sine, cosine, and logarithm—have derivatives
that
aren’t so simple. For natural logarithms and exponentials, here are the rules:
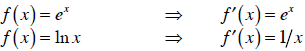
| Prev | Next |