Review of Basic Matrix Operation
Review of Basic Matrix Operations
Reading:
Appendix C of the text.
The matrix math supplement to Appendix C ¨C a handout available at 123 Latrobe
Hall.
Review your linear - algebra textbook as required
Show your work. Don't just write down the final answer - be methodical and clear
about the entire
sequence of steps you used to arrive at your answers.
Given the following matrices
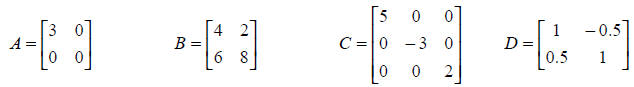
1. Compute by hand (show your work) the determinant,
eigenvalues, and eigenvectors of A. Check your
result ¨C verify that 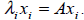
2. Compute by hand (show your work) the determinant, eigenvalues, and
eigenvectors of B. Check your
result ¨C verify that 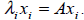
3. Compute by hand (show your work) the determinant, eigenvalues, and
eigenvectors of C. Check your
result ¨C verify that 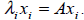
4. Compute by hand (show your work) the determinent, eigenvalues, and
eigenvectors of D. Check your
result ¨C verify that 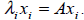
5. Use Matlab to compute the eigenvalues of A. Print your work.
6. Use Matlab to compute the eigenvalues of B. Print your work.
7. Use Matlab to compute the eigenvalues of C. Print your work.
8. Use Matlab to compute the eigenvalues of D. Print your work.
| MATLAB Function Reference eig Eigenvalues and eigenvectors |
Go to function: |
Search Help Desk Examples See Also |
Syntax
d = eig(A)
[V,D] = eig(A)
[V,D] = eig(A,¡¯nobalance¡¯)
d = eig(A,B)
[V,D] = eig(A,B)
Description
d = eig(A) returns a vector of the eigenvalues of matrix A.
[V,D] = eig(A) produces matrices of eigenvalues (D) and eigenvectors (V) of
matrix A, so that A*V
= V*D. Matrix D is the canonical form of A--a diagonal matrix with A's
eigenvalues on the main
diagonal. Matrix V is the modal matrix--its columns are the eigenvectors of A.
The eigenvectors are scaled so that the norm of each is 1.0. Use [W,D] = eig(A¡¯);
W = W¡¯ to
compute the left eigenvectors, which satisfy
W*A = D*W.
[V,D] = eig(A,¡¯nobalance¡¯) finds eigenvalues and eigenvectors without a
preliminary balancing
step. Ordinarily, balancing improves the conditioning of the input matrix,
enabling more accurate
computation of the eigenvectors and eigenvalues. However, if a matrix contains
small elements that
are really due to roundoff error, balancing may scale them up to make them as
significant as the other
elements of the original matrix, leading to incorrect eigenvectors. Use the
nobalance option in this
event. See the balance function for more details.
d = eig(A,B) returns a vector containing the generalized eigenvalues, if A and B
are square
matrices.
[V,D] = eig(A,B) produces a diagonal matrix D of generalized eigenvalues and a
full matrix V
whose columns are the corresponding eigenvectors so that A*V = B*V*D. The
eigenvectors are scaled
so that the norm of each is 1.0.
Remarks
The eigenvalue problem is to determine the nontrivial solutions of the equation :
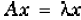
where A is an n-by-n matrix, x is a length n column
vector, and λ is a scalar. The n values of λ that
satisfy the equation are the eigenvalues , and the corresponding values of x are
the right eigenvectors.
In MATLAB, the function eig solves for the eigenvalues λ, and optionally
the eigenvectors x.
The generalized eigenvalue problem is to determine the nontrivial solutions of
the equation
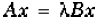
where both A and B are n-by-n matrices and λ is a scalar. The values of λ
that satisfy the equation
are the generalized eigenvalues and the corresponding values of x are the
generalized right
eigenvectors.
If B is nonsingular, the problem could be solved by reducing it to a standard
eigenvalue problem
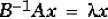
Because B can be singular, an alternative algorithm, called the QZ method, is
necessary.
When a matrix has no repeated eigenvalues, the eigenvectors are always
independent and the
eigenvector matrix V diagonalizes the original matrix A if applied as a
similarity transformation.
However, if a matrix has repeated eigenvalues, it is not similar to a diagonal
matrix unless it has a
full (independent) set of eigenvectors. If the eigenvectors are not independent
then the original matrix
is said to be defective. Even if a matrix is defective, the solution from eig
satisfies A*X = X*D.
Examples
The matrix
B = [3 -2 -.9 2*eps;-2 4 -1 -eps;-eps/4 eps/2 -1 0;-.5 -.5 .1 1];
has elements on the order of roundoff error. It is an example for which the
nobalance option is
necessary to compute the eigenvectors correctly. Try the statements
[VB,DB] = eig(B)
B*VB - VB*DB
[VN,DN] = eig(B,¡¯nobalance¡¯)
B*VN - VN*DN
Algorithm
For real matrices, eig(X) uses the EISPACK routines BALANC, BALBAK, ORTHES,
ORTRAN, and HQR2.
BALANC and BALBAK balance the input matrix. ORTHES converts a real general
matrix to Hessenberg
form using orthogonal similarity transformations. ORTRAN accumulates the
transformations used by
ORTHES. HQR2 finds the eigenvalues and eigenvectors of a real upper Hessenberg
matrix by the QR
method. The EISPACK subroutine HQR2 is modified to make computation of
eigenvectors optional.
When eig is used with two input arguments, the EISPACK routines QZHES, QZIT,
QZVAL, and QZVEC
solve for the generalized eigenvalues via the QZ algorithm. Modifications handle
the complex case .
When eig is used with one complex argument, the solution is computed using the
QZ algorithm as
eig(X,eye(X)). Modifications to the QZ routines handle the special case B = I.
For detailed descriptions of these algorithms, see the EISPACK Guide.
Diagnostics
If the limit of 30n iterations is exhausted while seeking an eigenvalue:
Solution will not converge.
See Also
| balance | Improve accuracy of computed eigenvalues |
| condeig | Condition number with respect to eigenvalues |
| hess | Hessenberg form of a matrix |
| qz | QZ factorization for generalized eigenvalues |
| schur | Schur decomposition |
| Prev | Next |