Preparation for Physics

Minimum Mathematical Background (Prerequisite: MA 106 or equivalent)
Required for PH 101-103 and PH 221-222 (with calculus)
by David G. Agresti, Professor of Physics, UAB
Bring to all classes: Scientific calculator and centimeter -based ruler and/or triangles.

1. Arithmetic

+ , - , × (or · ) , ÷ (or / ) , and powers

Examples: 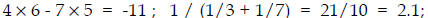Note order!

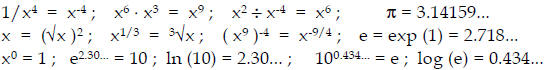
2. Scientific Notation

Powers of 10

Examples : 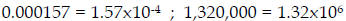(both have 3 sig. digits )

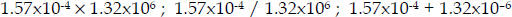
3. Geometry

Drawing and properties of 2 and 3-D figures

Examples:
Properties of rectangles, triangles, cylinders, spheres, etc.
Formulas for areas , volumes, perimeters of above
Angles in triangles and intersecting lines ; degrees and radians
Compass directions; vectors and vector operations (optional)

4. Trigonometry

Relations among sides (a, b, c) and angles (α, β) in a right (90°) triangle
Find missing information, given two sides or one side and an angle (≠90°)

Examples: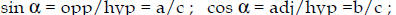

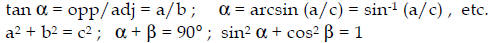
5. Graphing

2- and 3-D figures showing functional relationships and position in space

Examples:
Position coordinates in 2-D: (x, y) ; (r, θ)
Position coordinates in 3-D: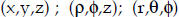
Functions of one and two variables: y = f (x); z = g (x, y)
Graphs of simple functions : 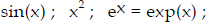  etc.

6. Algebra

Manipulation of expressions with variables

Examples: Addition of polynomials
Solving quadratic equations
Solving for unknowns in one or more equations
Note two rules for equations:
Do unto one side as you do unto the other.
N unknowns require N independent equations.

7. Proportions and ratios

Change in one variable when another one changes

Examples: Suppose a = b/c . Then, assuming the other quantity is constant:
Direct proportions are: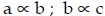 ; (read: "a is proportional to b")
Thus, e.g., if b is doubled, then a is doubled also.
Inverse proportion is: 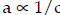; ("a is inversely proportional to c")
Thus, if c is doubled, then a is halved.
Ratios: Direct prop.: 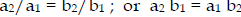  ( ratio is constant )
Inverse prop.: 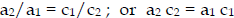  ( product is constant )

8. Use of the calculator

Scientific calculator is required.

Examples of calculator operations you should be able to perform:

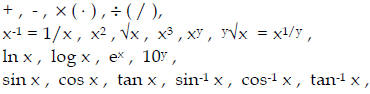
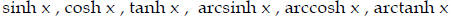(optional)

9. Calculus (required only for PH 221-222)

Simple derivatives, integrals, and related concepts,
including analytic geometry, limits, slopes, and extrema

Examples:
Derivatives of simple functions: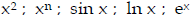
Graphical interpretation of slope ; rate
Maxima, minima, inflection points
Antiderivatives of simple functions
Definite integrals, area, volume