Ordinary Differential Equations and Linear Algebra

1. Separable Equations Revisited

Good Morning, everyone. I hope you all are feeling good about ODE. It is
one of the most fascinating subject of math I have ever studied. You have seen
many applications of ODE, we will see more along the way. Please let me know
if the pace is good for you.

Last time, we started talking about separable equations. It is the easiest
form of ODE you will encounter in this course. We will finish the rest of the
examples from last time.

Also you might be taught before that in 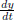, dy and dt are both just symbols ,
they are not really meaningful . But in that case, how can you separate them
also?

Here is another interpretation for way of solving separable equation.

Given the separable equation, 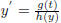, we have

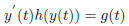
integrating both side, we get

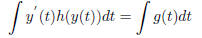
Notice that LHS is just a change of variable from ttoy . So the ODE is then
given by 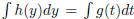Today we will be talking about another several
types of ODEs. We will start from linear equations .

2. First Order equation

Definition: A first-order equation is one of the form



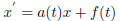
if f(t) ≡ 0, the equation is called homogeneous. Otherwise it is inhomogeneous.
Sometimes, the coefficient of x ' is not a constant, or not 1, i.e. it is of a more
general form



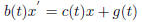
However, we should notice here the coefficient of x' and x are both in terms
of t only, the term like x ², xx' and cos x is not allowed by the definition of first
order equation. Here are several examples for you to judge whether they are
first order or not.

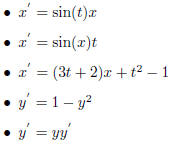
Now we want to know if there is some general way to solve the first order
equation. We start from the homogeneous ones.

We can do this in the very general setting as follows:

Given d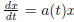, move the x terms to the left , and t term to the right as
we did in the separable equations. (this IS separable equation itself.)

we have

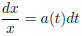
so

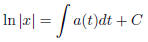
exponentiating, we get

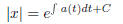
You can either keep this formula in mind or redo the above steps when you see it.

Here are a few practice examples.

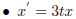
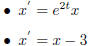(this is not a homogeneous equation)

From the above last problem, we see some inhomogeneous equation. This is
easy because it is also a separable equation. As the f(t) is a constant. We will
see the inhomogeneous equation could also be solved in general settings.

This is what is called the integrating factor method.

Namely, we introduce a integrating factor, we call it the
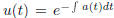
We then multiply both sides of the equation as follows.

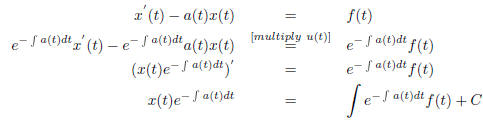
So then we solved the

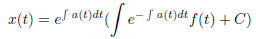
I have taught this method before . The feeling my students had is this is
not very natural. Yes, I admit this is a very creative and constructive idea.
Everything comes into such a beautiful form. What we can do here is just to
appreciate the beauty of math.

There are a few points you have to pay attention here.

1. We solve this in the general form



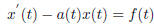
That means if you want to memorize the above formula, you will need to write
the given equation into the above form, and find what your a(t) and f(t) is.

2. As we did in studying calc II, we should not forget about the constant C.
Here the constant C is considered before you really write out the answer. That
would be a big mistake if you miss the constant.

3. However when we compute the integrating factors, we kind of need a simple
version of the many possible factors. So we just need to find ONE possible
integrating factor, without involving an extra constant in the integrating factor.

If you have the time and interests, you can try to verify the integrating factor
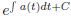with different choices of C’s could not affect your answer at all.

Here are a few examples to make you familiar with integrating factor method.

1. y' = −2y + 3 Here use 2 ways to find the solutions and check if they are
the same.

2.

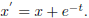
Solve:

a(t) = 1, and f(t) = e^-t. The integrating factor.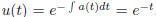
So according to our formula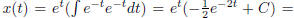


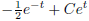
3. You can of course combine the initial value problem into the first order
equations.

Find the solution of



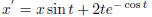
that satisfies x(0) = 1

4. find the general solution of x' = x tan t + sin t and also find the solution
that satisfies x(0) = 2.

Solve:

a(t) = tan t, and f(t) = sin t. The integrating factor is given by u(t) =


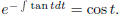
So we have 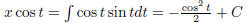So



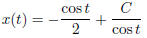
5. In class practice problem:



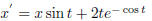
3. Structure of the solutions of first order ODE

Now you all have some feelings about this beautiful idea about integrating
factors. You may wonder why you distinguish the homogeneous and inhomogeneous
case. Are there any connections between these 2 cases. They are both
linear equations though.

You will see that more clear when you see matrix algebra . But now you can
still get a glimpse of the idea.

Look at the homogeneous equation



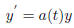
the solution is given by



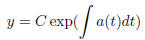
where the solutions for the inhomogeneous ones



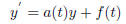
are given by

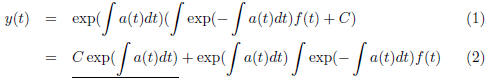
The underlined part is the solution of the homogenenous siblings.

Moreover, any solution of the inhomogeneous equation is the sum of a solution
from the homogeneous equation and a fixed special solution from the
inhomogeneous. i.e the solution of the inhomogeneous equation is given by



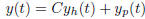
where 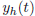is the solution of the homogeneous equation, where the 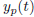is a
particular solution of the inhomogeneous equation.

3. Variation of Parameters:

Idea: you can always write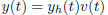

Example: y' = −2y + 3

4. Model of Motion:

Model of Motion with air resistence. The basic model is that the force of air
resistence is given by R(x, v) = −r(x, v)v where r is a nonnegative function.