Number Theory: Fermat's Last Theorem

Euclid, from
Elements

LEMMA 1
(before Proposition 29 in Book X)
To find two square numbers such that their sum is also a square.
Let two numbers AB , BC be set out, and let them be either both even or
both odd.

Then since, whether an even number is subtracted from an even number,
or an odd number from an odd number, the remainder is even [IX. 24, 26],
therefore the remainder AC is even.
Let AC be bisected at D.

Let AB, BC also be either similar plane numbers, or square numbers , which
are themselves also similar plane numbers.

Now the product of AB , BC together with the square on CD is equal to
the square on BD [II. 6].

And the product of AB, BC is square, inasmuch as it was proved that, if
two similar plane numbers by multiplying one another make some number the
product is square [IX. 1].

Therefore two square numbers, the product of AB, BC, and the square on
CD, have been found which, when added together , make the square on BD.

And it is manifest that two square numbers, the square on BD and the
square on CD, have again been found such that their difference, the product
of AB, BC, is a square, whenever AB, BC are similar plane numbers.

But when they are not similar plane numbers, two square numbers, the
square on BD and the square on DC, have been found such that their
difference, the product of AB, BC, is not square.
Q. E. D.

In order to translate Euclid’s argument into modern algebraic notation,
let AB = u, BC = v, CD = d, BD = f. From [II.6] Euclid obtains the
equation
uv + d² = f²,

which alternatively follows via
uv = (f + d)(f - d) = f² - d² ,

since D bisects AC and thus AD = CD = d.

The remainder of Euclid’s argument involves similar plane numbers. One
can prove that two numbers are similar plane numbers if and only if their
ratio is the square of a rational number (see the lemma at the end of the
section). Euclid continues his analysis by noting that uv is a square if and
only if u and v are similar plane numbers, which follows from the previous
sentence. So far he has given a procedure that beginning with two similar
plane numbers of the same parity constructs a Pythagorean triple. (The
parity of a number is simply whether it is even or odd. Thus 4 is of even
parity. That two numbers are of the same parity means that they are either
both even or both odd.) (Observe that his plane numbers must be unequal,
why?)

But in fact all Pythagorean triples arise in this way, as he somewhat
cryptically explains in the last paragraph. Start with a difference f ² - d²,
and factor it as uv, where u = f + d and v = f - d. Since this u and v are
clearly of the same parity, Euclid’s construction can proceed using these
numbers. Notice that this will reproduce the original d and f with which
we started. The result is the equation uv = f² -d² as above, but as Euclid
says in his last paragraph, this difference of squares, which is uv, will only
itself be a square if u and v were similar plane numbers to begin with.
Thus Euclid has set up a one-to-one correspondence between differences of
squares and pairs of unequal numbers of the same parity, in such a way that
differences of squares that are themselves square correspond to pairs that
are similar plane numbers. Thus he has classified all Pythagorean triples in
terms of similar plane numbers, so the problem of finding all Pythagorean
triples reduces to that of finding all pairs of similar plane numbers of the
same parity (Exercises 4.12–4.13).

Now we can see how to find the formulas of the Pythagoreans and Plato
that we mentioned. Since

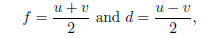
we have

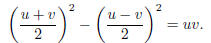
The simplest way to choose u, v such that their product is a square is to
let u = k² and v = 1. For f and d to be integers, we must have k odd, thus
leading to the formula of the Pythagoreans. Letting u = 2k² and v = 2
gives the Platonic formula [51, Vol. 1, p. 385].

From Euclid’s classification of Pythagorean triples we can derive the following
classification of all primitive Pythagorean triples, which we will need
for our next source. Suppose that the triple (d, e, f) is primitive. One of the
numbers d, e has to be even (this follows from Exercise 4.8 in the Introduction),
let us assume that it is e, by interchanging d and e if necessary. Now,
as noted above, we can apply Euclid’s method to this triple, obtaining

f² - d² = e² = uv,

with u, v similar plane numbers of the same parity. Thus u and v are both
even, and it follows from the lemma below that they are of the form u =
mp², v = mq². A common divisor of u and v also divides u + v = 2f and
u - v = 2d. But since d and f are relatively prime, that is, their greatest
common divisor is 1, it follows that the greatest common divisor of u and
v is 1 or 2. Together with the fact that u and v are even, this implies that
m = 2, and that p and q are relatively prime. Thus, the triple is of the form

d = p² - q², e = 2pq, f = p² + q² ,

and moreover, p and q have different parity , since d is odd by primitivity
of the triple.

To summarize, any primitive triple has this form (by interchanging d and
e if necessary), where p is greater than q, and p and q are relatively prime
and of different parity. Furthermore, any such choice of p and q results in
a primitive triple (check this).

Lemma: Two plane numbers are similar if and only if their ratio is the
square of a rational number.

Proof. Suppose that u and v are similar plane numbers. Then u = xy and
v = zw for some numbers (that is, positive integers ) x, y, z, w, which are
the sides of u and v, respectively. For these sides to be proportional means
that x = ry and z = rw for some rational number r. So

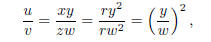
and y/w is clearly rational. Conversely, suppose u/v = (p/q)², where we
may assume that p and q are relatively prime. So

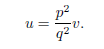
As u is an integer, we know that q² divides p²v. Since p and q are relatively
prime, q² must divide v, that is, v = mq² for some positive integer m.
Similarly, p² must divide u, and it is easy to see that in fact u = mp². If
we choose p and mp to be the sides of u, and q and mq to be the sides of
v, we see that u and v are similar plane numbers.

Exercise 4.11: Prove that there are only a finite number of Pythagorean
triples with a fixed leg.

Exercise 4.12: Show that there are exactly two pairs of similar plane
numbers of same parity that will produce a given Pythagorean triple using
Euclid’s construction.

Exercise 4.13: Enumerate (that is, give a recipe for listing) all pairs of
similar plane numbers with same parity. (Remember to show that your list
is complete.) Use your list to enumerate all Pythagorean triples.

Exercise 4.14: Enumerate all primitive Pythagorean triples.

Exercise 4.15: Derive a general formula from Diophantus’s treatment of
Pythagorean triples [86], and compare it with Euclid’s.

Exercise 4.16: Give a geometric demonstration of Euclid’s statement that
“the product of AB, BC together with the square on CD is equal to the
square on BD”, that is,

AB ٠ BC + (CD)² = (BD)²:

[Hint: Recall that the product of two numbers may be represented geometrically
as the area of a rectangle with those numbers as the lengths of its
sides.]

Exercise 4.17: Enumerate as many Pythagorean triples as you can that
contain the number 1378.

Exercise 4.18: In the two formulas for Pythagorean triples, ascribed to
the Pythagoreans and Plato, respectively, which triples, if any, appear on
both lists? Are the triples generated by these lists primitive? Which are,
and which are not? Are there an infinite number of primitive triples? Do
the primitive triples in the above two lists exhaust all possible primitive
triples?

4.3 Euler’s Solution for Exponent Four

Without doubt Leonhard Euler is one of the world’s mathematical giants ,
whose work profoundly transformed mathematics. He made extensive contributions
to many mathematical subjects, including number theory, and