More Exercises on Matrix Operations and Applications

1. Using Cramer’ s rule , find x₃ in the solution to the following system of equations:

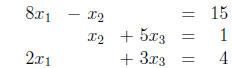
2. Multiply out the quadratic form 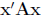in variables x ₁ and x₂ defined by
.
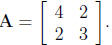
3. For the matrix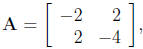

(a) Compute all the principal minors of A. What do these tell you about whether A
is positive or negative definite or semidefinite?

(b) Find the eigenvalues by finding all roots of the characteristic equation |A−rI| =
0. What do these tell you about whether A is positive or negative definite or
semidefinite?

(c) For the principal (largest) eigenvalue r₁ of A, find the eigenvector by finding a
solution to the system of equations (A − r₁I)h = 0. (Normalize this eigenvector
to have length 1.)

4. Consider a Markov process with two states in which:

• From state 1, an individual moves to state 2 with probability 3/4 and remains in
state 1 with probability 1/4;

• From state 2, an individual moves to state 1 with probability 1/2 and remains in
state 2 with probability 1/2.

For this process, do exercises (a) through (c) below:

(a) What is the transition matrix of this process?.

(b) In a large population whose individuals obey these transition probabilities in
periods t = 1, 2, . . ., suppose that at t = 1 half the population are in state 1 and
half are in state 2. What is the distribution across states at t = 2?