MATH 4073 Homework 4
Problem 1. Assume that the sequence
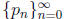 is generated by some iterative method
is generated by some iterative method
for finding a root of an equation . Also assume that we know that the sequence
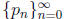
converges to some number p of some order α with some asymptotic error
constant λ, but
we don’t know the values of α and λ. The goal of this problem is to
develop a method
for determining the numerical value of α from the numerical values of the
members of the
sequence 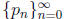 .
.
Let 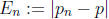 be the error at the nth step of the
iteration, and define
be the error at the nth step of the
iteration, and define 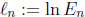 .
.
(a) Show that for large n, the following approximate identity holds:
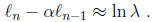
Hint: Just look at the definition of order of convergence .
(b) Using the approximate identity derived in (a) show that
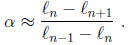
Note that this approximate formula for α does not depend on the base of the
logarithms;
if 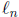 is defined as the log base 10 of
is defined as the log base 10 of
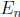 , the formula will remain the same.
, the formula will remain the same.
(c) The Mathematica notebook rate_of_convergence1.nb (which you can download
from the class website) computes the value of the solution of the equation sin
x+ x = 1
using (i) Newton’s method, (ii) the secant method, (iii) the fixed point
iteration
method, (iv) the fixed point iteration method combined with Aitken
extrapolation,
and (v) the fixed point iteration method combined with Steffensen’s method for
accelerating
convergence. Run all the programs from the notebook and use the formula
for α derived in part (b) to find empirically the numerical values of α
for all these
methods. Does the values of α you have obtained match the theoretical
predictions?
Discuss briefly. One can prove (but you do not need to do this!) that the order
of
convergence of the secant method is
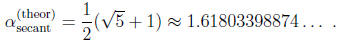
Note: Since we are using a very high accuracy (namely, 10000 digits), you have
to be
patient when runnig the programs; make sure that a program is finished before
you
run the next one. There is no need to attach the printout of running the
programs –
it will be too long. Give only the numbers that you use and show your
calculations
in detail. Recall that to perform some calculation in Mathematica , you need to
put
the cursor on that part of the program, press shift , and while holding it down,
press
return. Finally, note that in the notebook rate_of_convergence1.nb logarithms
base 10 are used.
Problem 2. In this problem you will develop a
modification the Newton’s method to find
a zero of multiplicity m ≥1 of the equation f(x) = 0.
(a) Let the sequence 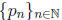 be defined by the
recurrence relation
be defined by the
recurrence relation 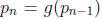 (and
(and
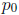
is some initial guess), where 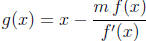 . Prove that,
if the point p is a zero of
. Prove that,
if the point p is a zero of
multiplicity m of f, then g'(p) = 0. This implies that the sequence
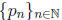 converges
converges
faster than linearly .
Hint: The calculations you need to do are very similar to the ones on pages
80–81 of
the book involving the function μ(x).
(b) Find the multiplicity of the root 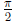 of the
equation
of the
equation 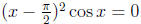 .
.
(c) The following Mathematica code similar to the codes from Problem 1

can be used (after an appropriate modification) to find empirically the order of
convergence
of the method. What is the order of the convergence that you observe? Explain
briefly your reasoning. (Again, be patient – Mathematica can take a while
because
you are doing the calculations with accuracy or 50000 decimal digits!)
(d) The number 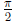 is a root of the equation
is a root of the equation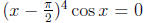 of multiplicity 5. Run the
of multiplicity 5. Run the
Mathematica code from part (c) after modifying it appropriately and use the
output
to find the order of convergence in this case. What do you observe?
(e) Modify the Matlab code newton.m to write a code newton_m.m that implements
the
algorithm from part (a) for finding zeros of multiplicity m of the equation f(x)
= 0.
The first line of your code must be
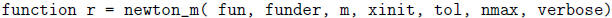
Note that in Matlab the name of a file must be the same as the name of the code
in it.
(f) One can estimate roughly the order of convergence m of an iterative method
as follows.
If after iterating enough number of times the error is significantly smaller
than 1 (say,
0.01 or smaller), then the number of correct digits of
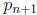 is roughly m times the
is roughly m times the
number of correct digits of
![]() . You can observe
this, in the following quadratically
. You can observe
this, in the following quadratically
convergent sequence (coming from using Newton’s method to find
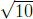 as in Problem 4
as in Problem 4
of Homework 3)

Give a theoretical explanation of this rule of thumb .
Hint: For example, in the number 3.162277665175674 . . . in the sequence above,
you
know the result with 8 correct digits after the decimal point, namely,
3.16227766;
the next one, 3.162277660168379335963284232 . . ., has 17 correct digits,
namely, the
correct digits are 3.16227766016837933. If you know a number
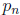 with k digits of
with k digits of
accuracy, what can you say about 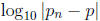 ?
?
Problem 3. Use the synthetic division algorithm to find consecutively the
following ratios:
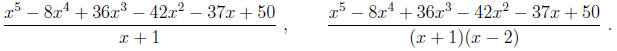
Use this result to find all roots (including the non- real ones ) of the
polynomial equation
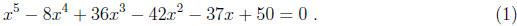
The built-in Matlab command roots finds ( possibly complex ) roots of polynomials.
The
argument of roots is a vector of all coefficients of the polynomial, starting
with the one at
the highest power . For example, to find all roots of the polynomial
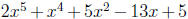 ,
,
type 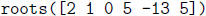 and press return. Use this command to
find the roots of
and press return. Use this command to
find the roots of
the polynomial equation (1) after you deflate it by eliminating the roots −1 and
2 (so that
you have to use roots to solve a cubic equation). Attach your Matlab printout.
Remark: One can find out more information about Matlab functions, say roots, by
typing
help roots
Use this to see the description of Matlab command fzero which is a built-in zero
finder. By
typing
help help
you will get information about the command help itself, and
help /
will give you a description of all operators and special characters.
Problem 4. Directly from the definition, find the rates of convergence α
and the asymptotic
error constants λ for each of the sequences (all of which tend to 0)
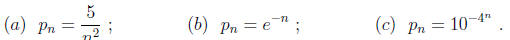
| Prev | Next |