Math 119 Pretest Review Questions
Linear Equations
Find the slope of the line passing through the given
points:
1. (2, -5); (0, 2)
2. (3, -4); (3, 0)
3. (-1, -2); (1, 4)
4. Find the equation of the line with slope 2 that
passes through (-2,-3). Write your answer in slopeintercept
form.
5. Find the general form of the equation of the line
that passes through (-1,6) and is parallel to the graph
of 2x + 3y − 4 = 0 .
6. Find the general form of the equation of the line
that passes through (4,-2) and is parallel to the graph
of x − y − 3 = 0 .
Quadratic Equations
Rewrite the following equations in general quadratic
form:
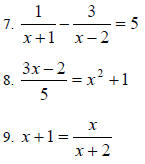
Complete the square for the following functions:
10. 2x2 − 8x + 5
11. − x2 − 4x − 7
12. 2x2 − 4x
Factor:
13. 4x3 y −16x2 y − 28y
14. x3 + 2x2 − 7x −14
15. 5xy2 + 5y2 + 3ax + 3a (Group in pairs)
16. (x + 3)3 −1
17. a3 − 64
18. 9y2 − 64
Finding Zeros/Roots
19. Use Descarte’s Rule of Signs to determine the
possible number of positive and negative zeros :
f (x) = x3 +1
20. Given f (x) = x4 − 3x3 + x2 − 6x − 5 ,
determine the possible number of negative zeros.
21. List the possible rational zeros of the function :
f (x) = 3x5 + 2x2 − 3x + 2
22. List the possible rational zeros of the function:
f (x) = 4x3 + 3x2 − 5x + 6
23. Use the fact that i is a zero of f to find the
remaining zeros:
f (x) = x4 − 5x3 + 7x2 − 5x + 6
24. Find all of the zeros of the
function: f (x) = x4 + 25x2 +144
25. Find all the real zeros of the polynomial function:
g(t) = t3 + 3t2 −16t − 48
26. Use the Intermediate Value Theorem to estimate
the real zero in the interval [1, 2]:
− 3x4 + 2x3 − x2 + x + 2
27. Use the Intermediate Value Theorem to estimate
the real zero in the interval [3, 4]:
2x3 − 5x2 − 7x +11
28. Use the Intermediate Value Theorem to estimate
the real zero in the interval [0, 1]:
3x3 + 7x − 9
Long and Synthetic Division
29. Find all of the real roots:
2x3 + 5x2 − x − 6 = 0
30. Find all of the real zeros of the function:
f (x) = 2x3 − 7x2 + 7x − 2
31. Write as a product of linear factors:
f (x) = x4 − 6x3 − 4x2 + 40x + 32
32. Simplify the rational expression:
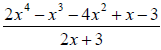
33. Simplify the rational function:
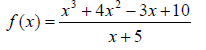
34. Simplify:
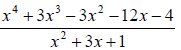
Absolute Value
Solve the following equations for x:
35. |x − 3| = 2
36. |x| = 5
37. |x + 5| = −1
Simplify the following expressions involving
absolute values:
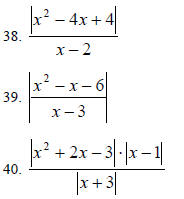
Pythagorean Theorem
For questions 41-42, consider a right triangle with
sides of length a, b, and c:
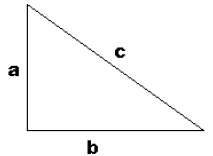
41. If the lengths of sides a and b are six and eight
inches respectively, how long is side c?
42. What is the length of side b in terms of the sides a
and c?
Distance Formula
Find the distance between the given points:
43. (2, 5); (-1,9)
44. (-1, 3); (5,1)
45. (10, -3); (3, 0)
Simplifying Expressions
Simplify:
46.
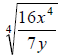(Assume all variables represent positive
real numbers)
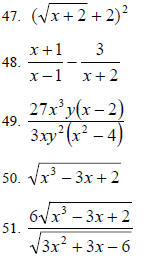
Rationalize the denominator and simplify:
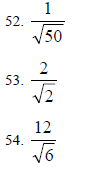
Solving Equations
Solve for x or y:
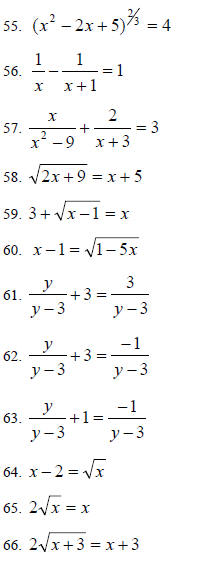
Inequalities
67. x > 3x − 2
68. 3x < 4x +1
69. x −1 ≤ 3x + 2
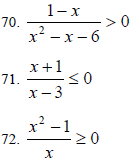
73. x2 +1 > x + 3
74. x3 − 2x2 + 6x + 3 ≤ x2 +10x + 3
75. x2 − 4x + 4 < x3 − 6x2 +11x − 5
Solve each absolute value inequality:
76. |x − 3| < 2
77. |x + 5| ≤ 0
78. |x + 2| ≥ 3
Logarithmic, Exponential and Logistic Functions
79. Write as the logarithm of a single quantity:
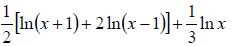
| Prev | Next |