LINEAR EQUATION

HOMEWORK 1.1: 8,14,20,24,46,26*,36* (Problems with * are recommended only and are not turned in).

SYSTEM OF LINEAR EQUATIONS . A collection of linear equations is called a system of linear equations.
An example is

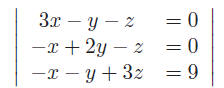
This system consists of three equations for three unknowns x, y, z. Linear means that no nonlinear terms like
x², x³, xy, yz³, sin(x) etc. appear. A formal definition of linearity will be given later.

LINEAR EQUATION. The equation ax+by = c is the general linear equation in two variables and ax+by+cz =
d is the general linear equation in three variables. The general linear equation in n variables has the form
a₁x₁ + a₂x₂ + ... + a_nx_n = a₀ . Finitely many of such equations form a system of linear equations.

SOLVING BY ELIMINATION .
Eliminate variables . In the first example, the first equation gives z = 3x − y. Substituting this into the
second and third equation gives

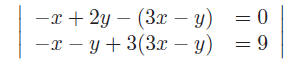
or

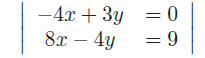
The first equation leads to y = 4/3x and plugging this into the other equation gives 8x− 16/3x = 9 or 8x = 27
which means x = 27/8. The other values y = 9/2, z = 45/8 can now be obtained.

SOLVE BY SUITABLE SUBTRACTION .
Addition of equations . If we subtract the third equation from the second, we get 3y − 4z = −9 and add
three times the second equation to the first, we get 5y − 4z = 0. Subtracting this equation to the previous one
gives −2y = −9 or y = 2/9.

SOLVE BY COMPUTER.
Use the computer. In Mathematica:

Solve[{3x − y − z == 0,−x + 2y − z == 0,−x − y + 3z == 9}, {x, y, z}] .

But what did Mathematica do to solve this equation? We will look in this course at some efficient algorithms.

GEOMETRIC SOLUTION.

Each of the three equations represents a plane in
three-dimensional space. Points on the first plane
satisfy the first equation. The second plane is the
solution set to the second equation. To satisfy the
first two equations means to be on the intersection
of these two planes which is here a line. To satisfy
all three equations, we have to intersect the line with
the plane representing the third equation which is a
point.

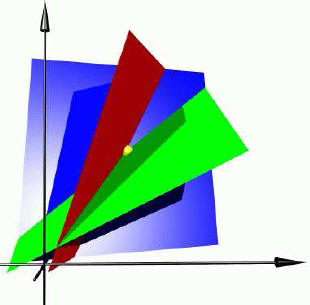
LINES, PLANES, HYPERPLANES.
The set of points in the plane satisfying ax + by = c form a line.
The set of points in space satisfying ax + by + cd = d form a plane.
The set of points in n-dimensional space satisfying a₁x₁ + ... + a_nx_n = a₀ define a set called a hyperplane.

RIDDLES:

”25 kids have bicycles or tricycles. Together they
count 57 wheels. How many have bicycles?”

Solution. With x bicycles and y tricycles, then x+
y = 25, 2x + 3y = 57. The solution is x = 18, y = 7.

”Tom, the brother of Carry has twice as many sisters
as brothers while Carry has equal number of sisters
and brothers. How many kids is there in total in this
family?”

Solution If there are x brothers and y sisters, then
Tom has y sisters and x−1 brothers while Carry has
x brothers and y − 1 sisters. We know y = 2(x −
1), x = y − 1 so that x + 1 = 2(x − 1) and so x =
3, y = 4.

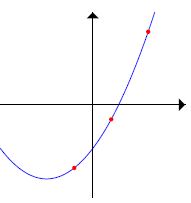
INTERPOLATION.

Find the equation of the
parabola which passes through
the points P = (0,−1),
Q = (1, 4) and R = (2, 13).

Solution. Assume the parabola con-
sists of the set of points (x, y) which
satisfy the equation ax^2 + bx + c = y.
So, c = −1, a+ b + c = 4, 4a+ 2b + c =
13. Elimination of c gives a + b =
5, 4a + 2b = 14 so that 2b = 6 and
b = 3, a = 2. The parabola has the
equation 2x^2 + 3x − 1 = 0

TOMOGRAPHY
Here is a toy example of a problem one has to solve for magnetic
resonance imaging (MRI). This technique makes use of the ab-
sorbtion and emission of energy in the radio frequency range of
the electromagnetic spectrum.

Assume we have 4 hydrogen atoms, whose nuclei are excited with
energy intensity a, b, c, d. We measure the spin echo in 4 different
directions. 3 = a + b,7 = c + d,5 = a + c and 5 = b + d. What
is a, b, c, d? Solution: a = 2, b = 1, c = 3, d = 4. However,
also a = 0, b = 3, c = 5, d = 2 solves the problem. This system
has not a unique solution even so there are 4 equations and 4
unknowns .

INCONSISTENT. x − y = 4, y + z = 5, x + z = 6 is a system with no solutions. It is called inconsistent.

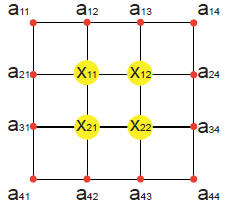
EQUILIBRIUM. As an example of a system with many
variables, consider a drum modeled by a fine net. The
heights at each interior node needs the average the
heights of the 4 neighboring nodes. The height at the
boundary is fixed. With n^2 nodes in the interior, we
have to solve a system of n^2 equations. For exam-
ple, for n = 2 (see left), the n^2 = 4 equations are

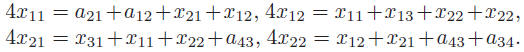
To the right, we see the solution to a problem with
n = 300, where the computer had to solve a system
with 90′000 variables.

LINEAR OR NONLINEAR?
a) The ideal gas law PV = nKT for the P, V, T , the pressure p, volume V and temperature T of a gas.
b) The Hook law F = k(x − a) relates the force F pulling a string extended to length x.
c) Einsteins mass-energy equation E = mc^2 relates restmass m with the energy E of a body.

ON THE HISTORY. In 2000 BC the Babylonians already studied problems which led to linear equations.
In 200 BC, the Chinese used a method similar to Gaussian elimination to solve systems of linear equations.