Lecture VII - Number Theory
Number theory encompasses anything relating to properties of integers. In
contests, we
typically encounter problems involving divisibility and factorization. In this
lecture we will
let p1, p2, . . . represent the prime numbers in ascending order so that pn is
the nth prime
number. We let gcd(p, q) represent the greatest common denominator and let lcm(p,
q) the
least common multiple of integers p and q.
1 Divisibility and Factoring
The Fundamental Theorem of Arithmetic says that any positive integer n can be
represented
in exactly one way as the product of prime numbers, so that the factorizations
of p and q
are identical if and only if p = q.
The number f divides n if and only if none of the powers of the primes in the
factorization
of f are greater than those of n. Specifically, f divides n k times if and only
if there is no
prime p is the factorization of f that appears more than 1/k times as often as
it appears in
the factorization of n.
On a related note, if some integer f divides integers p and q, then f divides
mp + nq,
where m and n are any integers.
Quick question: How many times does 3 divide 28!?
We reason that the answer is the sum of how many times 3 divides each of 1,
2, . . . , 28. Of the
numbers 1 through 28, exactly
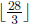 a multiples of 3,
a multiples of 3,
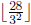 are multiples of 3^2, etc. (where
are multiples of 3^2, etc. (where
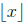
is the floor function and represents the greatest integer less than or equal to
x). To count the
total number of p’s appearing in their factorizations, we compute 9+3+1+0+0+0+·
· · = 13.
The generalized result:
Theorem : Aprime number p divides n! exactly
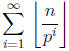 times.
times.
This fact enables us to determine how many 0’s appear at the end of n!.
Because there
are more 2’s than 5’s in the factorization of n!, the number of 0’s at the end
of n! is the
number of 5’s in its factorization.
Quick question: How many factors does 120 have?
We factor 120 and find that 120 =
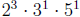 .
Therefore, any m =
.
Therefore, any m =
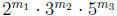 that
that
divides 120 must satisfy
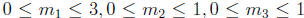 .
There are 4 possible m1, 2
.
There are 4 possible m1, 2
possible m2, and 2 possible m3, meaning that there are 4 · 2 · 2 = 16 positive
integers that
divide 120. Moreover:
Theorem :
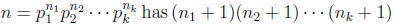 factors.
factors.
The greatest common divisor of m and n is defined to be the largest integer
that divides
both m and n. Two numbers whose largest common divisor is 1 are called
relatively prime
even though neither m nor n is necessarily prime. There are two notable ways to
compute
gcd(m, n).
• Factoring - Let
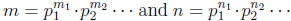 such that
such that
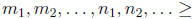
0. Then gcd(m, n) is the positive integer whose prime factorization contains pi
exactly
min(mi, ni) times for all positive integers i. Remark - This is useful if the
factorizations
of m and n are readily available, but if m and n are large numbers such as 4897,
they
will be difficult to factor.
• Euclidean Algorithm - Let n > m. If m divides n, then
gcd(m, n) = m. Otherwise,
gcd(m, n) = gcd(m, n − m · 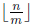 ). Remark - This
is useful when factoring
). Remark - This
is useful when factoring
fails. For example, finding gcd(4897, 1357). 1357 does not divide 4897, so
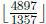 = 3,
= 3,
4897 − 3 · 1357 = 826 and gcd(4897, 1357) = gcd(1357, 826). 826 does not divide
1357, so gcd(1357, 826) = gcd(826, 531). 531 does not divide 826 so gcd(862,
531) =
gcd(531, 295). Continuing this process, gcd(531, 295) = gcd(295, 236) = gcd(236,
59) =
59.
The least common multiple of m and n is defined to be the
least number that is divisible
by both m and n. Other than listing multiples of m and n, we can determine the
lcm by the
formula : lcm(m, n) = 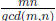 . Note that because
gcd(m, n) ≥ 1, we have lcm(m, n) ≤ mn.
. Note that because
gcd(m, n) ≥ 1, we have lcm(m, n) ≤ mn.
The Euler Phi function, 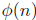 ,
denotes the number of positive integers less than or equal
,
denotes the number of positive integers less than or equal
to n that are relatively prime to n. If we let
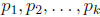 denote all of the distinct prime
denote all of the distinct prime
numbers that divide p, then:
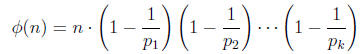
2 Modulo Trickery
The division algorithm states that when dividing n by p ≠
0, there is exactly one integer q
such that n = pq + r, where 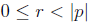 . We define n
modulo p (or simply m mod p) to be
. We define n
modulo p (or simply m mod p) to be
r in this equation . We use the notation r 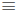 n
(mod p) when solving equations . There are
n
(mod p) when solving equations . There are
a number of theorems that apply to modulos, some of which are outlined here:
• k · n + c 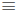 c (mod n),
for any integers k, n, and c. This follows from the definition
c (mod n),
for any integers k, n, and c. This follows from the definition
of modulos.
• 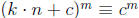 (mod n), for any
integers k, n, and c, and any positive integer m.
(mod n), for any
integers k, n, and c, and any positive integer m.
This is the result of binomial expansion of the left side.
• 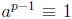 (mod p), for
relatively prime integers a and p, where p is prime. A result
(mod p), for
relatively prime integers a and p, where p is prime. A result
known as Fermat’s Little Theorem.
• 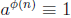 (mod n), for any
relatively prime integers a and n, where
(mod n), for any
relatively prime integers a and n, where 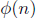 is
the Euler
is
the Euler
Phi function. This is Euler’s Generalization of Fermat’s Little Theorem.
• (p − 1)! 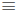 −1 (mod p),
for any prime p. This is Wilson’s Theorem.
−1 (mod p),
for any prime p. This is Wilson’s Theorem.
Whenever the word remainder appears, you should
immediately think modulos. Likewise,
determining the last few digits of a number should make you consider modulos.
The above theorems are merely suppliments to the algebra
that can be performed on
modular equations, which we outline here. The rules of modular arithmetic can be
summarized
as follows:
1. The only numbers that can be divided by m in modulo n
are those that are multiples
of gcd(m, n).
2. When multiplying by m in modulo n, the only numbers
that can result are multiples
of gcd(m, n).
3. Taking the square root of both sides is “normal” only
in prime modulos. (For example,
the solutions to 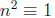 (mod 8) are not only
(mod 8) are not only
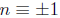 (mod 8) but more completely
(mod 8) but more completely
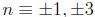 (mod 8).)
(mod 8).)
4. When solving for integer solutions in modulo n, any
integer multiple of n can be added
to or subtracted from any number. (This includes adding multiples of n to square
roots
of negative numbers.)
5. All other operations behave normally according to the
standard rules of algebra over
the integers.
Consider, for example, solving for all positive n ≤ 100
for which 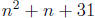 is divisible by
is divisible by
43. Of course we set up 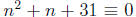 (mod 43). We apply
the quadratic formula and
(mod 43). We apply
the quadratic formula and
find that 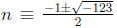 (mod 43). Because −123
(mod 43). Because −123
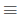 −123 + 43k (mod 43), we replace
−123 + 43k (mod 43), we replace
-123 with −123 + 5 · 43 = 49 and continue: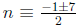 (mod 43), so n
(mod 43), so n 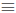 3,−4 (mod 43).
3,−4 (mod 43).
Therefore, all such n are 3, 39, 46, 82, and 89.
3 Practice
All of the following problems can be solved with the techniques enumerated above.
1. How many factors does 800 have?
2. How many times does 7 divide 100!?
3. What is the smallest positive integer n for which
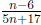 is non-zero and reducible?
is non-zero and reducible?
4. In Mathworld , the basic monetary unit is the Jool, and
all other units of currency are
equivalent to an integral number of Jools. If it is possible to make the
Mathworld
equivalents of $299 and $943, then what is the maximum possible value of a Jool
in
terms of dollars ?
5. What are the last three digits of
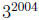
6. Compute the remainder when 2000! is divided by 2003.
7. (ARML 1999) How many ways can one arrange the numbers
21, 31, 41, 51, 61, 71, and
81 such that any four consecutive numbers add up to a multiple of 3?
8. Determine all positive integers n ≤ 100 such that
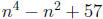 is divisible by 73.
is divisible by 73.
| Prev | Next |