Inverse Functions
Short Answer: If f (x) = x, its inverse (under the
operation of function composition)
is just itself, i.e. 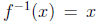 . Why? Because
. Why? Because
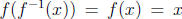 and
and 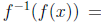
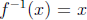 . A more substantive example is better, such
as the function f : (0,∞) defined
. A more substantive example is better, such
as the function f : (0,∞) defined
by f (x) = x2. Then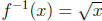 because
because 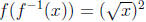 and
and 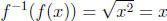
for all x in (0,∞).
Long Answer: To understand inverses we must first understand "identitites." For
any
algebraic operation , the identity is that which leaves things unchanged under
the operation.
For example, under addition the right identity is 0 because a + 0 = a for any
number
a. That is, adding 0 to a on the right doesn't change a . Similarly, for
multiplication, 1 is
the right identity, because multiplying any number on the right by 1 leaves that
number
unchanged; i.e. a ·1 = a. Sometimes we can find a left identity too. For example,
the left
identity under addition is also 0 because 0 + a = 0 for any a. So 0 is both a
right and left
identity for addition. Similarly, 1 is both a right and left identity for
multiplication. When
it works on both sides it's called a two -sided identity, or just the identity.
Extend this idea now to the operation of matrix multiplication. Define
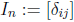 , where
, where
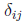 is the Kronecker delta,
is the Kronecker delta,
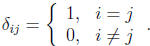
The equation 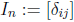 just says
just says
![]() is defined as the matrix whose entry in
the
is defined as the matrix whose entry in
the 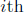 row and
row and
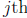 column is
column is 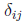 . In other words,
. In other words,
![]() is the n · n matrix with ones down the main
diagonal
is the n · n matrix with ones down the main
diagonal
and zeros everywhere else. For example,
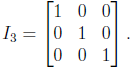
For all m · n matrices, the right identity is the matrix
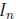 , because
, because 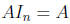 for
all m · n
for
all m · n
matrices A. Similarly, 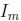 is the left identity, because
is the left identity, because
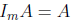 for all m · n
matrices. When
for all m · n
matrices. When
m ≠ n we cannot have a two -sided identity for matrix multiplication, because we
must
multiply on the left by an m · m matrix and on the right by an n · n matrix. So the
same
thing doesn't work on both sides. But for square n · n matrices, we do have a
two-sided
identity, just ![]() , because then
, because then 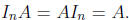 In an abuse of language, we usually call
In an abuse of language, we usually call
![]()
the n · n identity matrix, even if we're using it on non- square matrices .
Now that we understand identities, let's discuss inverses, which have the
following prop-
erty: operating on something with its inverse should give you back the identity
of that
operation. For example, the right inverse of the number 3 under multiplication
is 1/3 , be-
cause 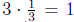 , which is the multiplicative identity . Note that 1/3 is also its left inverse
, which is the multiplicative identity . Note that 1/3 is also its left inverse
because 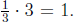 Since it works on both sides, it's called a two -sided inverse, or just
the
Since it works on both sides, it's called a two -sided inverse, or just
the
inverse of 3 under multiplication. Note that the inverse of 1 under
multiplication is just
itself, 1, because 1 ·1 = 1 = 1 ·1. Now consider addition. The (two-sided) inverse
of 3 is
-3 because -3 + 3 = 0 = 3 + (-3). Similarly, the inverse of the additive
identity 0 is just 0
itself because 0 + 0 = 0 = 0 + 0. Similarly, the inverse of
![]() is
is
![]() because
because
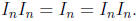
So the inverse of the identity is just the identity. This
is true in general: the inverse of the
identity is just the identity itself.
Inverses for addition and multiplication are easy enough, but what about
inverses for the
operation of function composition? This is a little more abstract. To figure out
what the
inverse is under composition, we first have to ask ourself what the identity is.
Consider all
functions with domain A and codomain B. The identity is just the function f : A
→ B
defined by f (x) = x, because it leaves what you put in unchanged. Now that we
know
what the identity is, what is the inverse of a function under function
composition? Like I
said in class, it is the function
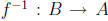 such that
such that
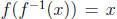 for all
x in B and
for all
x in B and
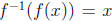 for all x in A. A simple example is
for all x in A. A simple example is
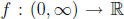 defined by f (x)
= x2.
defined by f (x)
= x2.
Then its inverse is 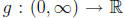 defined by
defined by 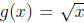 because
because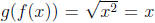 and
and
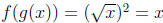 for all x in (0,∞). That is, the functions g o f and f o g are both the
for all x in (0,∞). That is, the functions g o f and f o g are both the
identity function, and therefore we can say that g = f -1.
Make sense? If you have any questions, please let me know.
| Prev | Next |