Fractions
In a fraction, the number above the bar is called the
numerator and the number below the bar
is called the denominator.
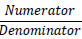
Fractions can be used to indicate parts of a whole:
Also, we use fractions to indicate division:
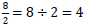
*Note:
Simplifying Fractions
A fraction is in lowest terms when no integer other than 1
will divide both its numerator and its
denominator exactly.
Examine: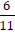 
and
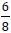
We can simplify (or reduce) a fraction that is not in
lowest terms by
dividing its numerator and its denominator by the same number. For
example:
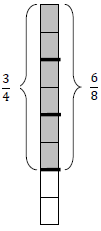
Visually you can see that
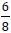and
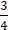are equal fractions:
When a composite number has been written as the product of
other natural numbers, we say
that it has been factored. When a composite number is written as the
product of prime
numbers, we say that it is written in prime-factored form.
Examine: 15=_______·_______
Example 1: Write 210 in prime-factored form.
Example 2: If possible, simplify:
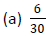
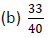
The Fundamental Property of Fractions : If a ,b, and x are real numbers ,
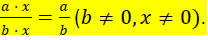
Multiplying Fractions: To multiply fractions, we multiply
their numerators and multiply their
denominators. In Symbols, if a, b ,c, and d are real numbers,
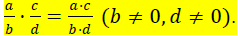
For example,
Fractions whose numerators are less than their
denominators are called proper fractions.
Fractions whose numerators are greater than or equal to their denominators are
called
improper fractions.
Example 3: Perform each multiplication.
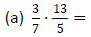
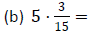
Example 4: Out of 36 students in a history class,
three-fourths have signed up for a trip to
Europe. If there are 28 places available on the flight, will there be room for
one more student?
Dividing Fractions
One number is called the reciprocal of another if their product is 1.
Consider 
what is the reciprocal?
Dividing Fractions: To divide two fractions, we multiply the first fraction by
the reciprocal of
the second fraction. In symbols, if a, b ,c, and d are real numbers,
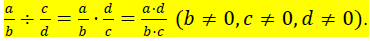
Example 5: Perform each division:
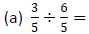
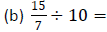
Adding Fractions with the Same Denominator: To add
fractions with the
same denominator, we add the numerators and keep the common
denominator. In symbols, if a ,b, c, and d are real numbers,
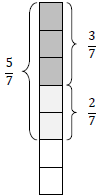
For example,
To add fractions with unlike denominators , we write the
fractions so that they have the same
denominator, in particular, the least common denominator (LCD). The LCD
is found by
examining the prime-factorization of each denominator and using each prime
factor the
greatest number of times it appears.
For example: If 5 and 3 are denominators of two fractions we want to add,
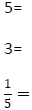
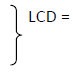
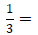
So,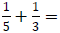 
Example 6: Add: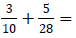 
Subtracting Fractions with the Same Denominator: To
subtract fractions with the same
denominator, we subtract their numerators and keep their common denominator. In
symbols,
if a, b, and d are real numbers,
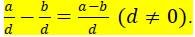
To subtract fractions with unlike denominators, we write
them as equivalent fractions with a
common denominator.
Example 7: Subtract 5 from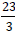 
.
Mixed Numbers
A mixed number represents the sum of a whole number and a fraction.
Example 8: Add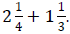 
Example 9: How much fencing will be needed to enclose the area within the triangular lot?
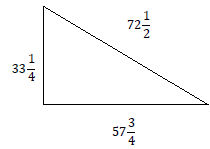
Decimals
Every rational number can be changed into either a terminating decimal or
repeating decimal.
| Terminating Decimals | Repeating Decimals |
 |
 |
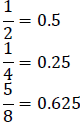To add or subtract decimals we align their decimal points
and then add or subtract:
To multiply decimals we multiply the numbers and place the decimal point so that
the number
of decimal places in the answer is equal to the sum of the decimal places in the
factors.
To divide decimals we move the decimal point in the divisor to the right to make
the divisor a
whole number. We then move the decimal point in the dividend the same number of
places to
the right.
Rounding Decimals
Rounding Decimals:
1. Determine to how many decimal places you wish to round.
2. Look at the first digit to the right of that decimal place.
3. If that digit is 4 or less, drop it and all digits that
follow. If it is 5 or greater, add 1 to the
digit in the position to which you wish to round, and drop all digits that
follow.
Applications
A percent is the numerator of a fraction with a denominator of 100. For
example,
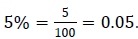
Example 10: Juan signs a one-year note to borrow $8,500 to
buy a car. If the rate of interest is
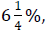how much interest will he pay?
| Prev | Next |