Formal Methods Key to Homework Assignment 3, Part 2
• Prove that multiplication of rational numbers is
well-defined.
Proof. Suppose m, n, p, q, r, s, t and u are integers such that n, q, s,
and u are nonzero,
m/n = r/s, and p/q = t/u. We want to see that
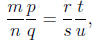
or, equivalently
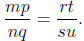
From the definition of equality of rational numbers , we need to see that
mpsu = nqrt.
But by assumption m/n = r/s and p/q = t/u. So ms = nr and
pu = qt. Substituting
into the left-hand side of the equation mpsu = nqrt, we get
nrqt = nqrt.
Reversing the steps , then, we see that
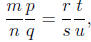
and multiplication of rational numbers is well -defined.
89. Is the converse of “if n is any prime, then 2n + 1 prime” true? If your
answer is yes,
prove the statement. Otherwise find a counterexample.
The converse is “if 2n + 1 is prime, then n is prime.” This is false. For
example,
24 + 1 = 17, but 4 isn’t prime.
94. Prove that if a and b are rational numbers with a < b, then there exists a
rational
number r such that a < r < b.
Proof. Define r = (a+b)/2. Then if m, n, p, and q are
integers with n and q nonzero,
such that a = m/n and b = p/q, we have
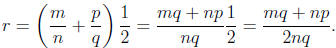
Since mq + np is an integer and 2nq is a nonzero integer,
we see that r is a rational
number.
To check that a < r < b, we can check that the differences r − a and b − r are
both
positive. We have that
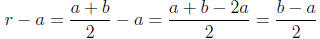
Since a < b, we know that b−a > 0. So r −a > 0 and a < r.
The argument that b−r
is positive is entirely analogous:
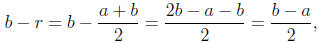
which, as we’ve just seen is positive. So r is a rational
number such that a < r < b.
95. Prove that if x is a positive real number , then x + 1/x ≥ 2.
Proof. This is similar to problem 80, which we proved by contradiction. So let’s
try
assuming the contrary. That is, we assume that x is a positive real number such
that
x+1/x < 2. Since x is positive, we can multiply both sides of this inequality by
x and
get
x2 + 1 < 2x,
or, equivalently ,
x2 − 2x + 1 = (x − 1)2 < 0.
However, since x is a real number (x − 1)2 ≥ 0, and this is
a contradiction. So the
assumption that x + 1/x < 2 must be false, and x + 1/x ≥ 2 for all positive real
numbers x.
96. (a) Find positive real numbers x and y such that
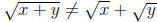 .
.
If x = y = 1, then x and y are positive, and 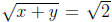 but
but 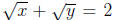 .
.
Since 2 is rational and 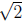 is irrational,
is irrational,
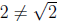 .
.
(b) Prove that if x and y are positive real numbers, then
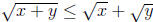 .
.
First Proof. We’ve proved a number of inequalities involving real numbers by
using contradiction. So let’s try contradiction. So we assume that x and y are
positive real numbers such that
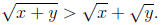
Since the function f(z) = z2 is increasing on the positive reals, we know that if
0 < a < b then 0 < a2 < b2. So
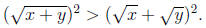
Simplifying , gives
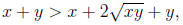
and subtracting x + y from both sides gives
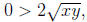
but since x and y are positive reals,
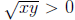 . So
. So 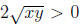 ,
which is a contradiction.
,
which is a contradiction.
So the assumption that
![]() must be false, and
we have
must be false, and
we have
that ![]() , for all
positive real numbers x and y.
, for all
positive real numbers x and y.
Second Proof. We can reverse the steps in the argument given in the first proof
and give a direct proof of the the result. Suppose that x and y are positive
real
numbers. Then 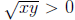 , and
, and
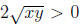 . Thus
. Thus
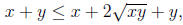
or, equivalently,
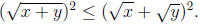
Since the function 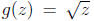 is
increasing on the positive reals, we can take
is
increasing on the positive reals, we can take
square roots of both sides of this inequality, and get
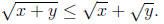
Note. Since 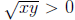 , this
proof actually shows that
, this
proof actually shows that
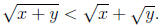
| Prev | Next |