Factoring Polynomials
The process of factoring a polynomial is analogous to the
process of factoring
an integer into its prime factors. For example 180 factors as 22325. We want
to do the same thing, but with polynomials.
Factoring out the Greatest Common Factor
Example. 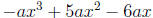
Factoring by Grouping
Method : Group terms in pairs depending on whether they have common
factors, then factor out common term .
Example. 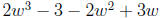
Example. −10z + 6yz + 5 − 3y
Factoring polynomials of the form ax2 + bx + c
Polynomials of this form (degree 2) are called quadratic polynomials .
Method: Find two numbers whose sum is b and whose product is ac. Replace
b by the sum of these two numbers, and factor the resulting polynomial by
grouping.
Example. 12b2 + 17b + 6
Example. x2 − 4x − 12
Factoring Special Products
1) Difference of Two Squares a 2 − b2 = (a + b)(a − b)
2) Perfect Square Trinomial a2 + 2ab + b2 = (a + b)2
3) Perfect Square Trinomial a 2 − 2ab + b2 = (a − b)2
4) Difference of Two Cubes a 3−b3 = (a−b)(a2+ab+b2)
5) Sum of Two Cubes a 3+b3 = (a+b)(a2−ab+b2)
Example. 9t2 − v2
Example. 4w2 − 4w + 1
Example. 9x2 − 12xy + 4y2
Example. m3 + n3
Example. a3 − 8
Example. 8t3h3 + n9
Factoring Completely
Example. a4b2 − 16b2
Example. a3 + a2 − 4a − 4
Example. −36x3 + 18x2 + 4x
Example. a7 − a6 − 64a + 64
| Prev | Next |