Exponents and Polynomials
Section 4.1 Exponents and Their Properties
An exponential expression is an expression that has
a base and an exponent –
baseexponent. The base can be a constant, variable, or algebraic expression.
We evaluate this expression by writing it in expanded form and using repeated
multiplication. The base is repeated as a factor for the number of times
represented by the
exponent.
When the base contains variables, we can utilize the properties of exponents to
help us
simplify the exponential expression.
Properties of Integer Exponents
For any base a and b and nonnegative integer exponents n and m,
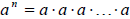for n factors of a
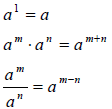
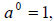where
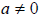
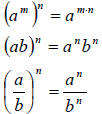
Section 4.8 Negative Exponents and Scientific Notation
When an exponential expression contains negative integer exponents, it is
standard, in
most cases, to transform the expression to have only positive integer exponents.
To do
this, we need some more rules.
More Properties of Integer Exponents
For any base a and b and nonnegative integer exponents n,
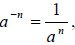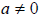
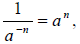where
where
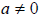
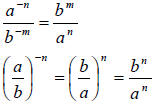
Scientific Notation
A number is said to be in scientific notation when
expressed in the form N ×10m , where
1≤ lNl < 10 and m is any integer. The number N is called the mantissa and m the
characteristic of N ×10m .
Scientific notation is used to express very large and very small numbers. When
solving a
problem where one of the inputs is in scientific notation, it is customary to
express the
answer in scientific notation.
To express a large number in scientific notation
1. Move the decimal point to the left until there is only one digit to the left
of the
decimal point.
2. Drop zeros from the right until you reach the first non-zero number. The
resulting
number is the mantissa, N.
3. The characteristic, m, is the number of decimal places the decimal point was
moved to the left. In this case, m is a positive integer.
4. Express the result as N ×10m .
To express a small number in scientific notation
1. Move the decimal point to the right until there is only one non-zero digit to
the
left of the decimal point.
2. Drop all zeros to the left of the new decimal place. The resulting number is
the
mantissa, N.
3. The characteristic is the number of decimal places the decimal point was
moved
to the right. In this case, m is a negative integer.
4. Express the result as N ×10-m .
To convert a number in scientific notation back to decimal notation also
requires moving
the decimal point.
• If the characteristic m is positive, move the decimal point m decimal places
to the
right. Place zeros in all place-values that do not contain numbers in them.
• If the characteristic m is negative, move the decimal point m decimal places
to the
left. Place zeros in all place-values that do not contain numbers in them.
Shortcuts
• If the characteristic m is positive, add enough zeros to the right of the
mantissa so
that m digits occur after the decimal point, then move the decimal point to the
end
of the number.
• If the characteristic m is negative, add m zeros to the left of the mantissa
and place
a decimal point between the first two zeros.
Section 4.2 & Section 4.6 (Exercises 1-22) Polynomials
Recall that the terms of an expression are its addends (i.e. quantities
separated by plus or
minus signs). There are two types of terms.
• Constant terms, which represent only one number, and
• Variable terms , which represent different numbers
The numerical coefficient (or coefficient) of a term is its numerical factor.
When all of the terms in an algebraic expression contain the properties of:
1. Real number coefficients
2. Exponents on all variables are whole numbers
3. Variable terms do not appear in a denominator or under a radical
Then, the algebraic expression is called a polynomial.
Some polynomials are classified by the number of terms they contain. A monomial
is a
polynomial with one term, a binomial is a polynomial with two terms, and a
trinomial is
a polynomial with three terms. Polynomials with four or more terms have no
special
names. Thus, they are simply called polynomials.
The degree of a term in a polynomial is the sum of the exponents of its variable
factors.
The degree of a constant term is zero.
The degree of a polynomial is the largest degree of its terms. The term which
determines
the degree of the polynomial is called the leading term of the polynomial and
its
coefficient is called the leading coefficient.
The conventional method of writing a polynomial is to write the terms in order
of
decreasing degree. When a polynomial is written in this manner, it is said to be
in
descending order .
Simplifying Polynomials
Two terms are called like terms if:
1. They are both constant terms, or
2. Both variable terms contain the same variables with the same exponents on
each
variable.
We collect like terms in an algebraic expression in order to simplify
it. This
means that
we add the coefficients of the like terms, keeping the variable parts unchanged.
Evaluating Polynomials
A polynomial, like any algebraic expression, represents different values
depending on the
value(s) of its variable(s). To evaluate a polynomial, we substitute the value(s) of its
variable(s) into the expression, and then determine the value of the resulting
numeric
expression.
Section 4.3 & Section 4.6 (Exercises 23-34) Addition and
Subtraction of Polynomials
Addition of Polynomials
To add two polynomials enclosed in a set of parentheses :
1. Remove the parentheses, and then
2. Combine like terms
When we add two polynomials a horizontal or vertical format can be used.
To use the vertical format:
1. Rewrite each polynomial in descending order,
2. Arrange the polynomials with like terms in the same column, leaving spaces
for
any missing terms
3. Then combine the terms in each column.
The Opposite of a Polynomial
Recall that the opposite of a sum property of real numbers states the following
fact:
− (a + b) = −a + (− b). What this means is that if we want the opposite of an
expression,
we change the sign of every term in that expression. This is the same as
multiplying
every term by – 1.
Subtraction of Polynomials
Recall the definition for subtraction of real numbers: a − b = a + (− b). So,
since
polynomials have the same properties of real numbers, we can utilize this
definition for
the subtraction of polynomials.
To subtract polynomials enclosed in a set of parentheses:
1. Rewrite the subtraction problem as an addition problem using the definition
a − b = a + (− b).
2. Perform the addition.
Applications
Polynomials describe many situations in the real world. If we can find the
polynomial
that describes a particular situation, we can analyze the situation more closely
and then
make appropriate decisions regarding the situation.
Section 4.4 & Section 4.6 (Exercises 35-95) Multiplication
of Polynomials
To multiply a monomial by a monomial
1. Use the commutative and associative properties to rearrange factors
(constants
next to each other and variables next to each other)
2. Multiply the coefficients
3. Simplify the variable factors using the rules of exponents.
To multiply a polynomial by a monomial
1. Use the distributive law to multiply every term in the polynomial by the
monomial factor.
2. Simplify each term
3. Collect like terms
To multiply a polynomial by a polynomial
1. Use the distributive law to distribute every term of one factor to every term
of the
second polynomial factor.
2. Simplify each term
3. Collect like terms
Section 4.5 Special Products of Binomials
To multiply any two binomial factors
1. Use the distributive law to distribute each term of the first binomial factor
to the
second binomial factor as follows.
(a + b)(c + d ) = a(c + d )+ b(c + d )
2. Use the distributive law again as follows.
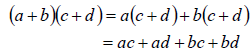
3. Simplify each term.
4. Collect like terms
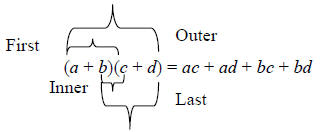
Sometimes, this process is called the FOIL method, where F stands for the first
terms, O
stands for the outside terms, I for the inner terms, and L for the last terms.
Graphically,
this looks like:
Special Binomial Products
Product of a Sum and Difference: (a.k.a. A Difference of Squares )
(A+ B)(A− B) = A2 − B2
Binomial Squares: (a.k.a. Perfect Square Trinomials )
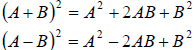
Section 4.7 Division of Polynomials
To divide a polynomial by a monomial
1. Use the distributive property of division, which is
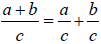
2. Simplify each term
3. Collect like terms
To divide a polynomial by a binomial
We can perform division of a polynomial by a binomial provided that the degree
of the
polynomial is greater than or equal to the degree of the binomial. This requires
a process
called polynomial long division, which is analogous to the long division of
arithmetic.
To perform polynomial long division of the expression a ÷b
1. Write the numerator and denominator in descending order.
2. Fill in any “missing terms”, using 0 for the coefficients.
3. Write the division problem into a long division format
.
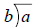4. Perform the division by determining what you must multiply the leading term
of
the binomial by to obtain the leading term of the polynomial.
5. Continue the division operation until
a. The remainder is 0, or
b. The degree of the remainder is less than the degree of the divisor.
6. Check your answer as follows: polynomial = binomial · quotient + remainder
| Prev | Next |