Exponential and Logarithmic Functions
Chapter 5 – Exponential and Logarithmic Functions –
Sections 5.1-6, 5.8
Composite functions
•Definition of function composition and associated notation
•Finding function compositions
•Finding the domain of a function composition
•Finding the components of a composite function
One-to-one functions; inverse functions
•Definition of the inverse of a function
•Definition of a one-to-one function
•Horizontal line test
•One-to-one functions and increasing or decreasing behavior
•Definition of an inverse function and associated notation
•Domain of f (x) equals range of 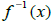 and range of
f (x) equals domain of
and range of
f (x) equals domain of 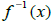
•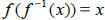 and
and 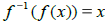
•The graph of a function and its inverse are symmetric over the line y =x
•Procedure for finding the inverse of a one-to-one function
Exponential functions
• Laws of exponents
•Definition of exponential function
•Graphing exponential functions
• Properties of exponential function 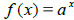
o Domain = all reals ; range = all positive reals
o No x- intercepts ; y-intercept = 1
o x-axis is a horizontal asymptote
o Is a one-to-one function
o For a>1, is an increasing function
o For 0<a<1, is a decreasing function
o Graph is smooth and continuous
•Definition of the number e
•Definition of the natural exponential function
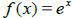
• Solving exponential equations by making bases the same
Logarithmic functions
•Definition of the logarithmic function to the base a,
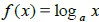
•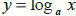 if and only if
if and only if
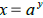
• Converting from log form equation to exponential form equation, or vice versa
•Finding exact values of log expressions
•Graphing log functions
•Properties of log function![]()
o Domain = all positive reals ; range = all reals
o No y- intercepts ; x-intercept = 1
o y-axis is a vertical asymptote
o Is a one-to-one function
o For a>1, is an increasing function
o For 0<a<1, is a decreasing function
o Graph is smooth and continuous
•Definition of and notation for the natural log function,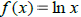
•Definition of and notation for the common log function,
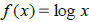
•Solving log equations by converting to exponential form
•Using logs to solve exponential equations
Properties of logs
•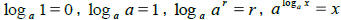
•Properties of logs: For M, N > 0, 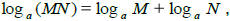
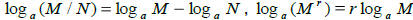
• Expanding single logs using properties of logs
• Combining log expressions into a single log using properties of logs
•Change-of- base formula
•Approximating logs using the change -of-base formula and a calculator
Logarithmic and exponential equations
•Solving log equations – convert to exponential form
•Exponential equations – take the log of both sides
Exponential growth & decay; Newton’s Law; logistic growth and decay models
•Exponential growth and decay models
•Population growth (bacteria, country populations, etc.)
•Radioactive decay (half-life, carbon-14 dating, etc.)
•Newton’s Law of Cooling
•Logistic growth models
Review Exercises
Chapter 5 Review Exercises: p. 336-9, 1-89, 93-97 odd
| Prev | Next |