Example of Newton's Method with Deflation and Horn
Problem: Find all solutions of
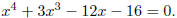
Solution : We’ll start with Newton’s method with p0 = 3. Set f(x) = x4+3x3−12x−16 and evaluate both this function and its derivative via synthetic division.
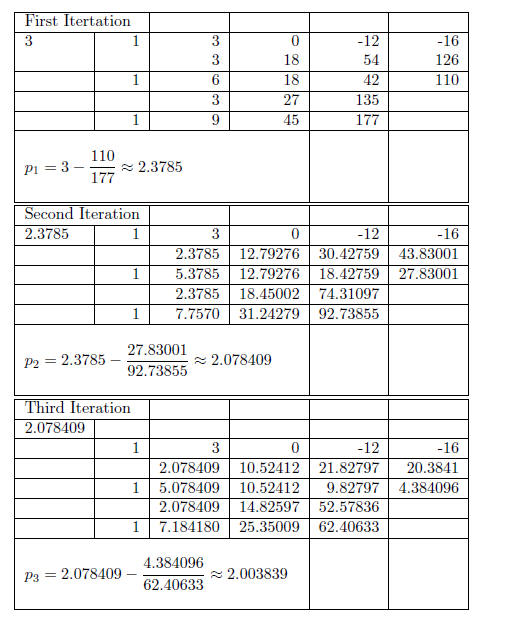
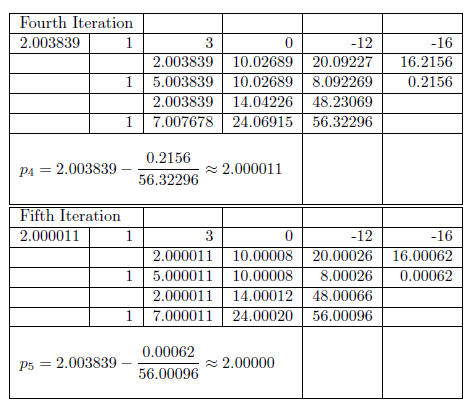
From the above table we are able to see that 2 is an
approximate solution , and
we also have the following factorization for our function :
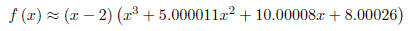
We’ll simplify the problem by looking for zeros of the
last factor. This is called
deflation.
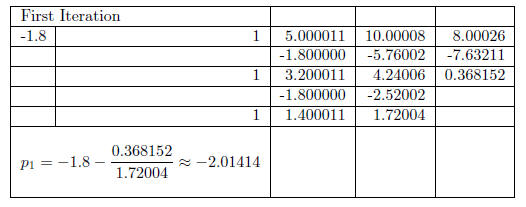
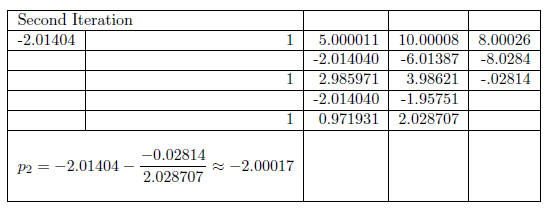
We now have another approximate solution and another factorization. Namely,
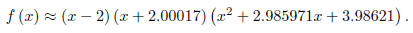
We’ll use the quadratic equation to find the last two zeros.
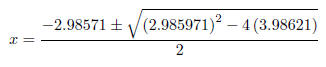
The two solution are −1.4929856 ± 1.3255958i
Errors accumulate in the coefficients during the deflation
process. We’ll use
Newton’s method with the original coefficients to refine the last three
solutions.
Again we use Horner’s rule for the calculations . The results are summarized
below.
Refinement of second solution : p2 = −2.00017, p3
= −2.000000022.
Refinement of third solution :
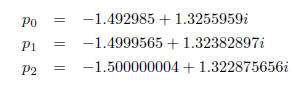
The fourth solution must be the complex conjugate of the
third solution. Finally,
we list the four approximate solutions :
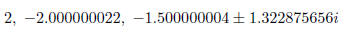
| Prev | Next |