Connecting Whole Number Arithmetic to Algebra
Description:
When students "hit" algebra, they are usually presented with concepts such as
"balancing"
equations, factoring and expanding polynomials , and linear equations. What
groundwork can be
set by the K-6- curriculum to lead students to see algebra as an extension of
their arithmetic skills?
Can the algebra curriculum bounce off students' previous knowledge of arithmetic
or must the
algebra curriculum start from its own frame of reference? Activities looking at
the operations on
whole numbers, using manipulatives and calculators, will be investigated and
then extended to the
"rules" of algebra. Share your thoughts on the question, "Can there be a
seamless journey from
arithmetic to algebra?"
Goals:
• Present a connection between the thought processes and algorithms developed
while
studying arithmetic and the thought processes and algorithms shown while
studying
algebra.
• Use word problems, investigations with manipulatives and calculators, and
finally the
written mathematics to present a connected route from arithmetic to algebra.
• Share thoughts on the question, “Can there be a seamless journey from
arithmetic to
algebra?”
In this Handout:
Part A: Word Problems: Natural Problem Solving and Inverse Operations
vs. Balancing Equations
Part B: Whole Number Algorithms and a Bit of Algebra!
Use Virtual Base 10 Blocks!
Part C: Multiplication Tables to Linear Equations
Part D: Using the TI-73 and the TI-Ranger to learn about lines!
Part A: Word Problems:
Balancing Equations vs . Natural Problem Solving and Inverse Operations
Addition and Subtraction:
1. Maggie had 5 cookies. Jamal gave her 3 more
cookies. How many cookies does Maggie have
altogether?
2. Maggie has 5 cookies. How many more cookies
does she need to have 8 cookies altogether?
3. Maggie had some cookies. Jamal gave her 5 more
cookies. Now she has 8 cookies. How many
cookies did Maggie have to start with?
4. Maggie had 8 cookies. She gave some to Jamal.
Now she has 5 cookies left. How many cookies did
Maggie give to Jamal?
Multiplication and Division:
1. If three children have two cookies each, how many
cookies are there altogether?
2. If two children have three cookies each, how many
cookies are there altogether?
3. If six cookies are shared among three children, how
many would each child get?
4. If there are six cookies and each child must get three
cookies, how many children can you serve?
Discussion Question:
Which should we teach? How do we link the processes?
| Balancing Equations | Natural Problem Solving and Inverse Operations |
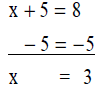 |
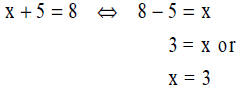 |
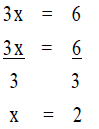 |
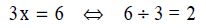 |
Part B: Whole Number Algorithms and a Bit of Algebra!
Using Base Ten Blocks to "See" Algorithms
Objective: To look at addition, subtraction, multiplication and
division of whole numbers from a
geometric, "hands-on" perspective and an algorithmic perspective.
Audience: This activity is intended for teachers. The activity is
designed to make connections
between the use of manipulatives and the development of algorithms. Parents and
students are
welcomed!
Part 1: Addition - Focus on trading and regrouping.
Part 2: Subtraction - Focus on trading and regrouping.
Part 3: Multiplication - Focus on the distributive property and area models.
Part 4: Division - Focus on the scaffold method and area models.
Part 5: A Bit of Algebra - Focus on the distributive property and area models.
Part 1: Addition
1. One Type of Addition Algorithm
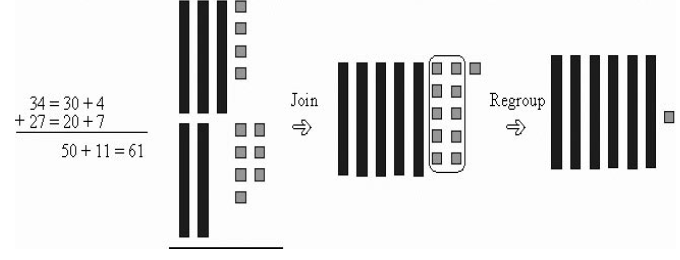
2. Try these problems using Base 10 Blocks and the algorithm. Write and draw your work .

Part 2: Subtraction
1. One Type of Subtraction Algorithm
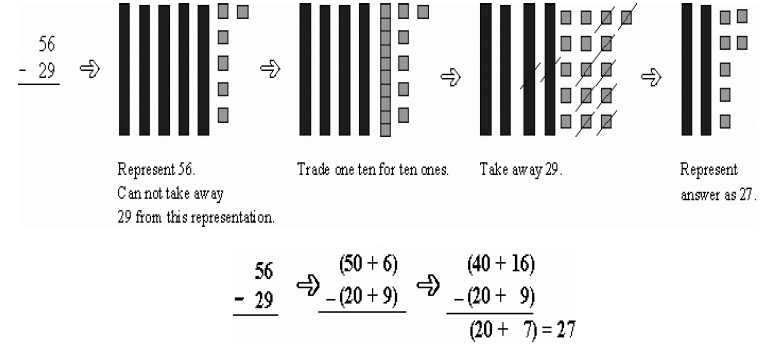
2. Try these problems using Base 10 Blocks and the algorithm. Write and draw your work.

Part 3: Multiplication
1. One Type of Multiplication Algorithm - If you have 23 students in
your class and they
each need 12 straws for a craft project, how many straws do you need to supply?
We
write this as 23 groups of 12 or 23 × 12. Write out how you would solve the
problem.
2. Notice two applications of the Distributive Property gives us the
"standard" pieces. Here
you see this in both vertical and horizontal formats. Find the pieces from the
computations
below on the area model. Notice that we are actually finding 12, 23's.
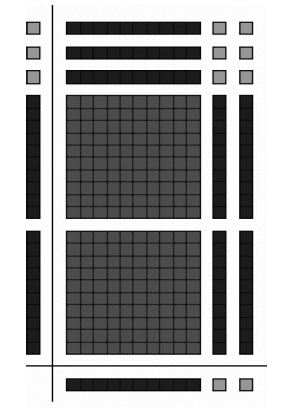
Vertical:
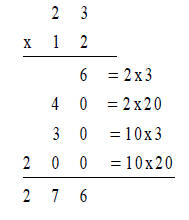
OR
Horizontal:
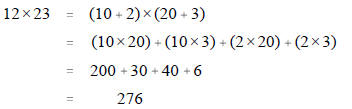
3. Try these problems using Base 10 Blocks. Draw or printout the area model
you construct.
Write out the details of the algorithm and find the products on your area model.
Notice
that the second problem is multi step. (Why?)

Part 4: Division
1. One Type of Division Algorithm - You have 483 sea shells for a
class art project.
Each student needs 21 shells. How many students will be able to make the
project? How
many groups of 21 shells can you form out of 483 objects? We write 483 ÷ 21.
Write
out how you would solve this problem.
2. Find the number of groups of 21 on the
Area Model. Draw in the left most column
with the appropriate “Base 10 blocks.”
3. Next, look at the scaffold method below.
(Is there a correlation to the scaffold “good
guess” method and the Area Model? Does
there have to be a relationship?)

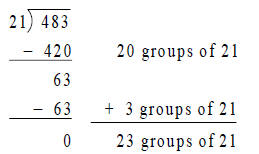
4. Now, you have 483 sea shells for a class art project. There are 21
students in your class.
If you give each student the same number of shells, how many shells will each
student
have? Use the blocks to model this problem. Is it still written 483 ÷ 21?
Discuss.
5. Caution: When you pick problems for illustration with Base 10 blocks, make
sure you
check them out first using the blocks! Sometimes a problem requires that you
break up a
FLAT in order to fill in the area model. This type of problem is not the best
for a first use
of the blocks.
Try these by drawing Base 10 Blocks. Solve also using the scaffold method.

Part 5: Moving to Algebra!
1. We can use the Base 10 blocks idea to create Base x
blocks or Algebra Tiles. x is unknown !
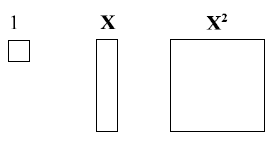
2. Look at the figure to the right. This is an area
representation of (x + 2)( x + 3). Compare this to
23 ×12. Do you see a similarity?
3. Expand:
(x + 2)( x + 3) =
Find the pieces on the picture to the right.
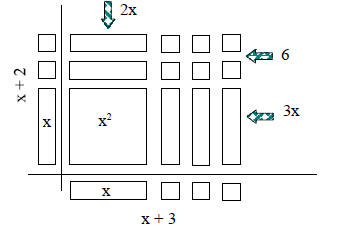
4. Try these! Draw them out and then expand. Can you see the pieces?
a. x(x+4)
b. (x+1)(2x+3)
c. Extension: Draw and expand (x + 2y + 3)(2x + y).
Hint: You will need y and y^2 blocks

Part C: Multiplication Tables to Linear Equations
You have no money now. You find out that you are going to get an allowance of
$2 each week.
You would like to buy a __________________ (Calculator) which costs ____________
($20). You will
save your money until you have enough! When will you have enough? How is your
money
growing?
1. With your group, decide how much money you will have week to week. Use the
table and
the graph below to organize your work.
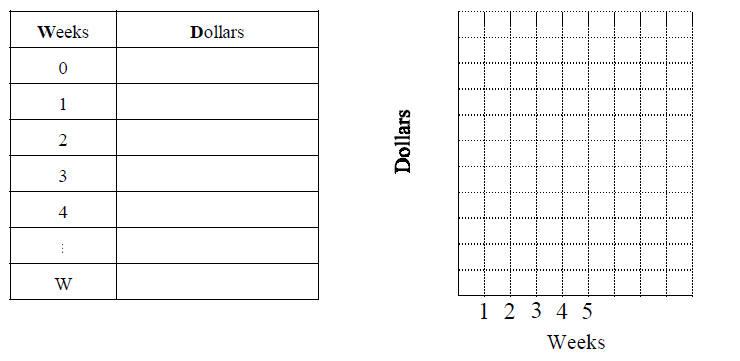
2. If you receive $2 each week you can write that in math symbols as____________________
3. Write the sequence of numbers that describes your money supply week to week.
____________________________________________________________
4. From your graph, write a word that describes the shape of the graph.____________________
5. Write a sentence to explain when you will have enough money to make your
purchase.
Write how you found this answer.
6. Use your work to predict the future! If you don’t spend any money for 14
Weeks, how
many Dollars will you have? Write an explanation of how you found your answer.
Use
words such as add, subtract, multiply, and divide.
Teacher’s Sheet
How Does Your Money Grow?
Classroom Organization:
Groups work and present their solution .
(Time saver - use overheads or small white boards for each table or have board
space for each group as they work.)
Discussions of Mathematics used in the solutions needs to occur.
Give the suggestion of the use of Tables of Numbers and Graphs as tools.
1. Reinforce multiplication as repeated
addition.

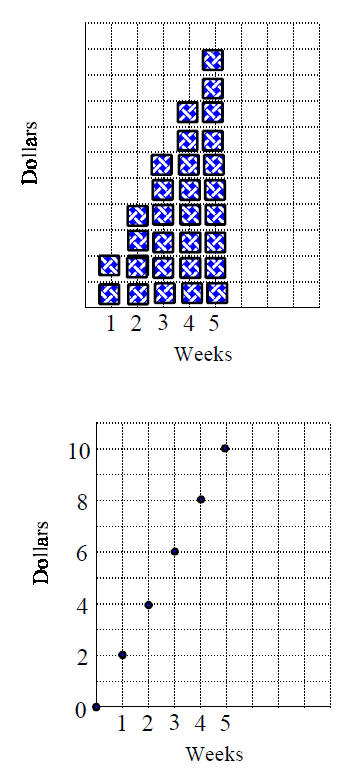
2. If you receive $2 each week you can write that in math symbols as
+2 , a constant rate of change
3. Write the sequence of numbers that describes your money supply week to
week.
2, 4, 6, 8, 10, This is an Arithmetic Sequence of numbers.
4. From your graph, write a word that describes the shape of the graph. a line
5. Write a sentence to explain when you will have enough money to make your
purchase.
Write how you found this answer.
Encourage students to see the relationship Dollars = 2 × Weeks This is developed
using
Inductive Reasoning.
Use of Division as an Inverse Operation:
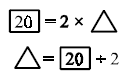
This sets the foundation of a function and an inverse function.
Students will also be able to read the answer from the table and the graph.
6. Use your work to predict the future! If you don’t spend any money for 14
Weeks, how
many Dollars will you have? Write an explanation of how you found your answer.
Use
words such as add, subtract, multiply, and divide.
Students can use the table, graph, the calculator to find the solution .
Encourage the
formal writing of Dollars = 2 × 14 = $28. Notice that if students use the table
or the
graph they will have to predict a pattern to use.
Added discussion: Commutative Property of ×
Does it matter?
Dollars = 2 × Weeks
or
Dollars = Weeks × 2
Part D: Using the TI-73 and the TI-Ranger to Learn about Lines!
Part I How Fast Do You Need To Go?
1. Use the Ranger program on your TI-73 to
collect data. A distance-time graph of
constant speed forms a straight line. Draw
your walk on the graph at the left. Write a
description of how you walked a constant
speed._____________________
2. How can you make your line steeper? _______________________________________________________________
3. Repeat the exploration above and walk a
distance-time graph which is steeper than your
first walk. Draw your walk on the graph.
4. Repeat the exploration above and walk a
steeper line. Draw your graph. What did you
have to do to get a steeper
line?_______________________________________________________________
5. Can you walk a line that is vertical (straight up and down)? Why or why not?
_______________________________________________________________
_______________________________________________________________
Part II How Fast Were You Going? Let's Look at Your Data!

1. Use the Ranger program on your TI-73 to gather data.
Walk a distance-time graph of constant speed. Draw your
walk on the graph.
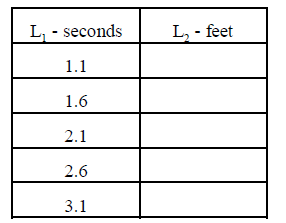
2. L1 is the time in seconds and L2 contains your position from Ranger. Fill
in the following
table with the data
3. The average velocity you walked can be
calculated by
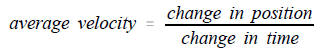
Use the information in the table to answer the
following questions.
4. How far did you walk from 1.1 sec to 1.6 sec?_________
This is your change in position.
5. How many seconds did you walk during 1.1 sec to 1.6
sec?_________
This is your change in time.
6. Your average velocity during 1.1 sec to 1.6 sec. is found by
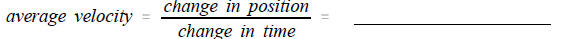
7. Find your average velocity during 1.6 sec to 2.1 sec.
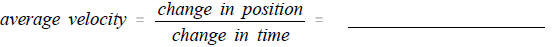
8. Find your average velocity during 2.1 sec to 2.6 sec.
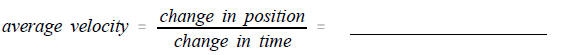
9. Find your average velocity during 2.6 sec to 3.1 sec.
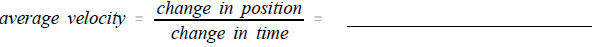
10. Did you come close to walking a constant speed? Explain your answer.
________________________________________________________________________________
11. How is the average velocity related to the slope of the distance -time line?
________________________________________________________________________________
12. What is the intercept of your walk ? How do you know?__________________________
13. Extension: Use Manual-Fit on the TI-73 to find
the equation that describes your walk.
Compare it to the linear regression line found by using LinReg on the TI-73!
| Prev | Next |