ADVANCED MATRIX OPERATIONS
ADVANCED MATRIX
OPERATIONS
• Advanced matrix operations fall under the
following categories
- Building larger matrices
- Relational operations
- Logical operators and functions
- Subscripting
- Manipulating matrices
- Reshaping
BUILDING LARGER MATRICES
• We can form larger matrices from smaller
matrices.
• Let a=[1 2 3;4 5 6;7 8 9] and b=[4 5 6] then
c=[a ,b’]
adds a 4th column to a.

MATRIX MULTIPLICATION
• MATLAB multiplies two matrices provided
rows and column numbers agree.
• For example, if
A=[1 2 3;4 5 6;7 8 9]
B=[7 8 9;4 5 6;1 2 3]
• Multiplication of A and B is simply A *B
18 24 30
54 69 84
90 114 138
RELATIONAL OPERATIONS
• Relational operators are defined as follows
< less than
<= less than or equal
> greater than
>= greater than or equal
= =equal
~= not equal
WHAT DO THEY DO?
• The response of a relational operator is
another vector
• This vector is binary (0,1) and of the same
length as the data vector
• The 1 locations indicate places where the
relational operator is TRUE
EXAMPLE USAGE
• Define the following row vector
v=[1 3 4 9 8 6 7 0 2]
• Do the following and look at the results.
x=v<5→ 1 1 1 0 0 0 0 1 1
x=v<=4 →1 1 1 0 0 0 0 1 1
x=v>3 →0 0 1 1 1 1 1 0 0
x=v>=0→ 1 1 1 1 1 1 1 1 1
x=v==6 →0 0 0 0 0 1 0 0 0
x=v~=6→ 1 1 1 1 1 0 1 1 1
EXACT LOCATION
IDENTIFICATION: find
• One of the most powerful operators in
MATLAB is find. It operates on a
vector/matrix and returns the positions of
nonzero entries
• find (v>=5) gives the exact locations where
the elements of v equal or exceed 5
• For v=[1 3 4 9 8 6 7 0 2 6]
- v>=5 ---- > 0 0 0 1 1 1 1 0 0 1
- find (v>=5) ------ >4 5 6 7 10
• The sum function is particularly powerful.
• If x is a vector, sum (x) is simply the sum of
the elements of x
- x=[1 3 4 2 6]
- sum (x)=16
• For a 2D array, sum (A) adds up each column

Combining sum and find
• Find how many times your data , stored in x,
exceeds a threshold
- x=[1 4 3 2 5 7 4 8 9 5 7];%data
- v=find (x>5);%{0,1} pointer array
- n=sum (v);%n equals number of 1's, i.e.
number of times x has exceeded 5
LOGICAL FUNCTIONS
• MATLAB contains a set of logical functions:
• any (x).....returns a 1 if any element in x is
nonzero
• all (x)....returns a 1 if all element in x are
nonzero
• find (x)..returns the indices of nonzero
elements of x
LOGICAL OPERATORS
• Logical expressions can be compared using
logical operators. There are 3 logical
operators:
not...~
and...&
or......|
• Define a=[1 9 8], b=[2 9 7] and c=[2 5 4 ]. Then
a>b=[0 0 1]
a>c=[0 1 1]
• Then a>b&a>c=[0 0 1].
ADVANCED SUBSCRIPTING
• You can pick out the elements of an array A
using another array
• Define
- A=[1 2 3;4 5 6;7 8 9],
- v=[1 3]
• Then A(:, v) is another matrix consisting of all
the rows of A but only columns 1 and 3.
• Try A (v,:)
ADDRESSING SPECIFIC
POSITIONS IN A MATRIX
• By using a logical array (0,1) we can point to
specific positions in a matrix.
• For example, let a=[1 3 4 9 8 7 7 0 2 8]. Want to
find values below 6
- v=a<6 ->1 1 1 0 0 0 0 1 1 0
- a(v) --> 1 3 4 0 2
A 2D example
• In an image processing application, we may
want to identify intensities above a threshold
in an image
- a=[7 6 3;6 5 2; 3 4 5];%input image
- v=a>5;%pointer to desired locations
- MATLAB responds v =
1 1 0
1 0 0
0 0 0
A(v) - - > 7 6 6
MAKING AN ARRAY OUT OF A
MATRIX
 |
•Using (:) by itself strings out all the elements of A in a long column vector |
• An interesting effect is generated by using A(:)=10:18 |
| • A(:)= 7 4 1 8 5 2 9 6 3 |
 |
|
EQUATING MATRICES
• It is important that when matrices or arrays
are equated, the number of rows and columns
match on both sides
• For example, if A is 3x3
- A=ones(4) is invalid because the left hand
side is 3x3 but the right hand side is 4x4.
• The correct assignment is
- A=ones(3)
EMPTY MATRICES
• Statement x=[] defines a zero x zero matrix.
This is different from clear x.
• We can use an empty matrix to efficiently
remove rows and columns from a matrix.
• The following removes columns 2 and 3
entirely

MATRIX MANIPULATION
• Here is a list:
- rot90...............rotation
- fliplr................flip matrix left to right
- flipud..............flip matrix up and down
- diag.................extract diagonal
- tril................... lower triangular part
- triu..................upper triangular part
- reshape...........reshape
REARRANGING MATRICES
• It is possible to rearrange , say, a 3x4 matrix
into a 2x6, 1x12, 4x3 etc. as long as number of
elements do not change
B=reshape(A,m,n)
maps A into an m rows, n columns matrix

reshape(A,2,8)
reshape PRACTICE
• Generate an alternating (+/-) 1 array of length
20 using reshape
[1 -1 1 -1 1 -1...1 -1]
• Hint: first create +1’s and -1’s separately, then
interleave them
USEFUL MATLAB FUNCTIONS
• The following functions are quite handy. Try
them on a random vector of numbers of
length 100.
- max (v)............find the maximum of v
- min (v)............find the minimum of v
- mean (v).........find the mean (average) of v
- std (v).............find the standard deviation
- sort (v)............sort v
- sum (v)...........sum of all the elements in v
- prod (v).......... product of elements in v
- hist (v)............histogram of values
Hands-on exercise
• Do the practices on Page 103 and 99
• The following 2 slides are also part of the
hands-on
Application note
l It is frequently desirable to isolate and
remove noisy spike in data
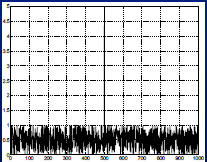
EXAMPLE: REPLACING AN
OUTLIER
• Want to locate a spike in data and then
remove it
- Load data file spike
- Plot the data
- Find out what position is the spike located at?
- Remove it and replace it by 0
- Plot your result to see if it has worked
WORKING WITH SOUND
• Let’s try out the previous commands on an
actual sound file.
• In the command window type load bond and
check your workspace to see where the data
went
• You can playback the sound file using sound
command
l Plot the sound file. Where is the data stored
in?
HOMEWORK
• After loading bond, write a code to do the
following tasks (one line per question! )
- Play bond backwards
- How many samples are in bond?
- The file is too big. Subsample it by half (keep every other sample)
- Find the peak amplitude and its location
- Find out locations in the array where m>0.8
- How many times does the signal amplitude exceed this threshold?
- Set all those amplitudes to 0.8
- Plot your result to verify
| Prev | Next |