The Quadratic Formula and the Discriminant
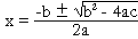is called the
quadratic formula . The quadratic formula can be used
to factor or solve any polynomial in the form : ax2 + bx + c where a ≠
0. When using the
quadratic formula, it is important to remember that there are three different
types of answers
you can get. The type of answer you will get depends on what the discriminant is
in the
problem. The discriminant is b2 - 4ac. You may see that it is
the part of the quadratic
formula that is in the square root. The three types of answers you can get with
the quadratic
formula are two real solutions , two imaginary solutions, or one real solution.
If the
discriminant is greater than zero , there will be two real solutions as in
examples one and two.
Example 1: 2x2 + 5x – 3 Discriminant = 49
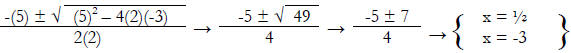
Example 2:
x2 + 5x + 3 Discriminant = 13
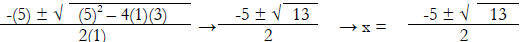
If the discriminant is less than zero, there will be two
imaginary solutions as in example
three.
Example 3: x2 – 4x + 5 Discriminant = -4
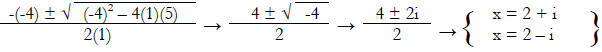
Finally, if the discriminant is equal to zero, then there
will be one real solution as in example
four.
Example 4: x2 – 6x + 9 Discriminant = 0
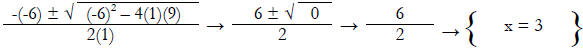
Sketching a graph:
To sketch a graph of a quadratic equation , you will need to find the vertex of
the
parabola , y-intercept, and x-intercepts.
To find the vertex, use the formula: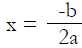
Then use the x- value in the original formula to find the y-value.
To find the y-intercept, set x = 0 and solve for y. The ordered pair will be the
y-intercept.
To find the x-intercept(s), set y = 0 and solve for x. You may get more
than one ordered pair. You can also use the quadratic formula to find the x-
intercepts.
To make the sketch, use the points that you found for the vertex, y-intercept,
and x-intercept(
s) and draw a curve through the points.
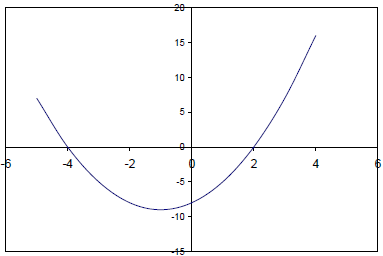
Example 5: y = x2 + 2x – 8
| Finding the x-intercept(s) | Finding the y-intercept | Finding the vertex |
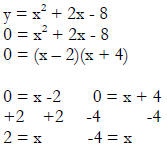 So the x- intercepts are (2,0) and (-4,0) |
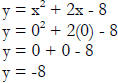 (0,-8) = y-intercept |
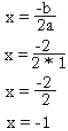 Now that we know what the x is, we can find the y-value. |
 |
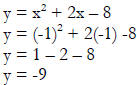 Vertex is (-1, -9) |
|
Sample Problems
For each of the following quadratic functions, find the vertex, y-intercept, and
the x-intercept(
s) of the parabola . Sketch the graph based on this information.
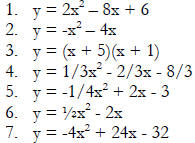
Use the quadratic formula to solve each of the following equations.
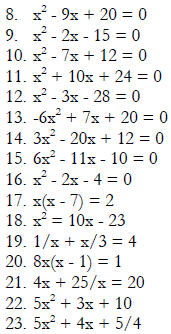
Solutions
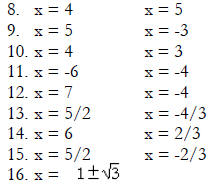
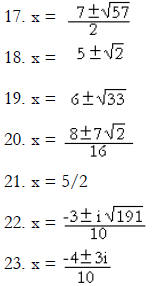
| Prev | Next |