Some Remarks on the Teaching of Fractions in Elementary School

The work done on the teaching of fractions thus far has come mainly
from the education community. Perhaps because of the recent emphasis on
situated learning, fractions tend to be discussed at the source, in the sense
that attention is invariably focussed on the interpretation of fractions in a
“ real world ” setting. Since fractions are used in many contexts in many
ways, students are led through myriad interpretations of a fraction from the
beginning in order to get some idea of what a fraction is. At the end, a
fraction is never defined and so the complexities tend to confuse rather than
clarify (cf. (2) at the beginning of the article). More to the point, such an
approach deprives students the opportunity to learn about an essential aspect
of doing mathematics: when confronted with complications, try to abstract
in order to achieve understanding. Students’ first serious encounter with the
computation of fractions may be the right moment in the school curriculum
to turn things around by emphasizing its abstract, simple component and
make the abstraction the center of classroom instruction. By so doing, one
would also be giving students a substantial boost in their quest for learning
algebra. The ability to abstract, so essential in algebra, should be taught
as early as possible in the school curriculum, which would mean during the
teaching of fractions. By giving abstraction its due in teaching fractions, we
would be easing students’ passage to algebra as well.

It takes no insight to conclude that two things have to happen if mathematics
education in K-8 is to improve: there must be textbooks that treats
fractions logically, and teachers must have the requisite mathematical knowledge
to guide their students through this rather sophisticated subject. I
propose to take up the latter problem by writing a monograph to improve
teachers’ understanding of fractions.

The first and main objective of this monograph is to give a treatment
of fractions and decimals for teachers of grades 5–8 which is mathematically
correct in the sense that everything is explained and the explanations are
sufficiently elementary to be understood by elementary school teachers. In
view of what has already been said above, an analogy may further explain
what this monograph hopes to accomplish. Imagine that we are mounting an
exhibit of Rembrandt’s paintings, and a vigorous discussion is taking place
about the proper lighting to use and the kind of frames that would show
off the paintings to best advantage. Good ideas are also being offered on
the printing of a handsome catalogue for the exhibit and the proper way
to publicize the exhibit in order to attract a wider audience. Then someone
takes a closer look at the paintings and realizes that all these good ideas might
go to waste because some of the paintings are fakes. So finally people see the
need to focus on the most basic part of the exhibit—the paintings—before
allowing the exhibit to go public. In like manner , what this monograph tries
to do is to call attention to the need of putting the mathematics of fractions
in order before lavishing the pedagogical strategies and classroom activities
on the actual teaching.

An abbreviated draft of the part of the monograph on fractions is already
in existence (Wu 1998). The main point of the latter can be summarized as
follows .

(i) It gives a complete, self-contained mathematical treatment of
fractions that explains every step logically.

(ii) It starts with the definition of a fraction as a number (a point
on the number line, to be exact), and deduces all other common
properies ascribed to fractions (cf. (a)–(e) above) from this definition
alone.

(iii) It explicitly and emphatically restores the simple and correct
definition of the addition of two fractions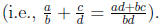

(iv) The four arithmetic operations of fractions are treated as extensions
of what is already known about whole numbers. This
insures that learning fractions is similar to learning the mathematics
of whole numbers.

(v) On the basis of this solid mathematical foundation for fractions,
precise explanations of the commonly used terms such as
“17 percent of”, “three-fifths of”, “ratio”, and “ proportional to ”
are now given.

(vi) The whole treatment is elementary and, in particular, is appropriate
for grades 5–8. In other words, it eschews any gratuitous
abstractions.

In the eighteen months since Wu (1998) was written, I have gotten to
know more about the culture of elementary school teachers and have come to
understand better their needs. I have also gotten to know, quite surprisingly,
that there are objections to a logically coherent mathematical treatment of
fractions in grades 5–8 by a sizable number of educators. This objection
would seem to be grounded on a misunderstanding of the basic structure
of mathematics. There are also some gaps in the treatment of Wu (1998).
All this new information must be fully incorporated into the forthcoming
monograph. More specifically, the envisioned expansion will address the
following areas:

(a) Discuss in detail from the beginning the pros and cons of the
usual “discrete” models of fractions, such as pies and rectangles,
versus the number line. Special emphasis will be placed on the
pedagogical importance of point (iv) above. Such a discussion
would address the concerns of many school teachers and educators
who are used to having “models” for an abstract concept
and have difficulty distinguishing between the number line as a
model for fraction and its use as a definition which underlies the
complete logical development of fractions.

(b) Explain carefully that at a certain point of elementary education,
a mathematical concept should be given one definition
and then have all other properties must be deduced from this
definition by logical deductions. This need is not generally recognized
in the education community. For fractions, the point in
question would seem to be reached in the fifth grade ([2]) or sixth
grade ([1]). Whether such logical deductions are properly taught
is likely to determine whether the learning of fractions is an immense
aid or obstacle to the learning of algebra later on.

(c) More clearly delineate which part of the exposition primarily
addresses teachers, and which part could be directly used in the
classroom. Early readers of Wu (1998) have been to known to
complain that “no student in the fifth grade could understand
the algebraic notation”, without realizing it was a document for
teachers.

(d) Add a treatment of negative fractions and complete the discussion
of the rational number system .

(e) Add a treatment of decimals and the relationship between
decimals and fractions. Emphasis will be placed on a precise
definition of decimals and the logical explanations of the common
properties of decimals, viz., why fractions are the same as
repeating decimals, and which fractions have finite decimal representations.

(f) Add a discussion of the role of calculators. Although calculators
already appear in the exercises at the end of §3 and §4 in
Wu (1998), there is need of a discursive and direct discussion of
this important issue.

(g) Amplify on the brief discussion of ratio and proportion in Wu
(1998). Carefully explain the unfortunate historical origin of the
concept of “ratio” in Euclid’s Elements which has led to immense
and unnecessary confusion about what it means. Clarify the concept
of so-called “proportional thinking” which has been treated
with unwarranted reverence in the literature.

(h) Add generous pedagogical comments on how to deliver such
an approach to fractions in the classroom.

(j) Expand on the rather terse expository style of Wu (1998), everywhere.
In particular more exercises and more examples are
needed.

Thus Wu (1998) will have to be fleshed out in a substantial way, and
its vision has to be sharpened. More importantly, to ensure its usefulness
as a resource for professional development, it is essential that it be tested
on teachers before it is finalized. Perhaps a draft of this mongraph can be
put into service in some professional development activities in the coming
months.