Solving Linear Equations Using a TI-89

Before you begin, clear all previously saved variables and functions , set the graph mode and
viewing window.

To Clear Home Screen
(Home if not on home screen)
F1 then 8

To Clear Previously Saved Variables
2^nd F6 then Enter Enter

To Clear Previously Saved Functions
Diamond Y=
F1 then 8 Enter

To Set Graph Mode
Mode (Graph is highlighted)
→ then 1 (Function)
Enter

To Set Graph Scale
Diamond Window
F2: Zoom
6: ZoomStd
F2: Zoom
5: ZoomSqr

Algebraically :

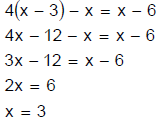
There are two ways to solve a linear equation graphically: Using Root and Using
Intersection

Graphically: Using Zero (Root)

Rewrite the equation with 0 on one side .
4(x − 3) − x − x + 6 = 0

Let Y1 equal the left side of the equation.

Diamond Y=
Y1 = 4(x − 3) − x − x + 6

Then graph.
Diamond Graph

Find the x- intercept (zero)
F5: Math
2: Zero
Lower Bound ?: - move cursor to the left of the x intercept using the left or right arrows
Enter
Upper Bound?: - move cursor to the right of the x intercept using the right arrow
Enter

At the bottom of the screen, it shows the x and y coordinate of the x intercept . (3, 0)

x=3 is the solution to the equation .

Graphically: Using Intersection

Each side of the equation represents a linear expression . If both sides of the equation are
graphed, their point of intersection has the same y value . Therefore, the x- coordinate of the
point of intersection represents the solution to the equation.

Graph both linear expressions :

Diamond Y=
(Clear functions)
Y1 = 4(x − 3) − x
Y2 = x − 6

Diamond Graph

To find the point of intersection:

F5: Math
5 Intersection
1^st Curve: (The cursor should be blinking on one line and the equation number will
appear in the upper right hand corner of the window. If you can’t see the cursor, use the
left or right arrows to bring it into view.)
Enter
2^nd Curve: (The cursor should move to the next line and the number will change to 2)
Enter
Lower Bound?: - move cursor to the left of the intersection using the right or left arrow
keys
Enter
Upper Bound?: - move cursor to the right of the intersection using the right arrow key
Enter

At the bottom of the screen, it shows the x and y coordinate of the point of intersection. (3, -3)

x=3 is the solution to the equation.