| Section 3.2

Solving Equations : The
Addition and Multiplication
Properties |
| Equation vs. Expression

Statements like 5 + 2 = 7 are called
equations.
An equation is of the form
expression = expression
An equation can be labeled as
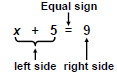
|
| Addition Property of Equality

Let a, b, and c represent numbers.
If a = b, then
a + c = b + c
and
a – c = b − c
In other words, the same number may be
added to or subtracted from both sides
of an equation without changing the
solution of the equation . |
| Multiplication Property of Equality

Let a, b, and c represent numbers and
let c ≠ 0. If a = b, then
a · c = b · c and 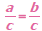
In other words, both sides of an
equation may be multiplied or divided
by the same nonzero number without
changing the solution of the equation. |
| Solve for x.

x − 4 = 3
To solve the equation for x, we need to rewrite
the equation in the form
x = number.
To do so, we add 4 to both sides of the
equation.
x − 4 = 3
x − 4 + 4 = 3 + 4 Add 4 to both sides.
x = 7    Simplify. Simplify. |
| Check

To check, replace x with 7 in the original
equation.
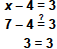 |
Original equation |
|
Replace x with 7. |
|
True. |
Since 3 = 3 is a true statement, 7 is the
solution of the equation. |
| Solve for x

4x = 8
To solve the equation for x, notice that 4
is multiplied by x.
To get x alone, we divide both sides of
the equation by 4 and then simplify .
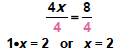
|
| Check

To check, replace x with 2 in the
original equation.
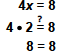 |
Original equation |
|
Let x = 2. |
|
True. |
The solution is 2. |
Using Both Properties to
Solve Equations

2(2x – 3) = 10
Use the distributive property to simplify
the left side.
4x – 6 = 10
Add 6 to both sides of the equation
4x – 6 + 6 = 10 + 6 4x = 16
Divide both sides by 4.
x = 4 |
| Check

To check, replace x with 4 in the original
equation.
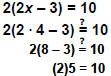 |
Original equation |
|
Let x = 4. |
| |
|
True. |
The solution is 4. |
| Section 3.3

Solving Linear Equations in
One Variable |
Linear Equations in One
Variable

3x - 2 = 7 is called a linear equation or
first degree equation in one variable.
The exponent on each x is 1 and there
is no variable below a fraction bar.
It is an equation in one variable
because it contains one variable, x. |

Make sure you understand which property
to use to solve an equation.
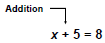
To undo addition of 5, we
subtract 5 from both sides.
x + 5 - 5 = 8 - 5
Use Addition Property of
Equality
x = 3 |
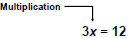
To undo multiplication of 3,
we divide both sides by 3.
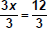
Use Multiplication Property
of Equality x = 4 |
|
| Steps for Solving an Equation

Step 1. If parentheses are present, use the
distributive property.
Step 2. Combine any like terms on each side of the
equation.
Step 3. Use the addition property to rewrite the
equation so that the variable terms are on
one side of the equation and constant terms
are on the other side.
Step 4. Use the multiplication property of equality to
divide both sides by the numerical
coefficient of x to solve .
Step 5. Check the solution in the original equation. |
Key Words or Phrases that translate to an
equal
sign when writing sentences as equations.

Key Words
or Phrases |
Sentences |
Equations |
|
equals |
5 equals 2 plus 3. |
5 = 2 + 3 |
|
gives |
The quotient of 8
and 4 gives 2. |
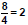 |
|
is/was/will be |
x is 5. |
x = 5 |
|
yields |
y plus 6 yields 15. |
y + 6 = 15 |
|
amounts to |
Twice x amounts to - 8. |
2x = - 8 |
|
is equal to |
36 is equal to 4 times 9. |
36 = 4(9) |
|
| Section 3.4

Linear Equations in One
Variable and Problem Solving |
| Problem-Solving Steps

1. UNDERSTAND the problem. During this step,
become comfortable with the problem.
Some ways of doing this are:
 Read and reread the problem. Read and reread the problem.
 Choose a variable to represent the Choose a variable to represent the
unknown.
 Construct a drawing . Construct a drawing .
 Propose a solution and check it. Pay Propose a solution and check it. Pay
careful attention to how you check your
proposed solution. This will help when
writing an equation to model the
problem. |
| Problem-Solving Steps . . .

2. TRANSLATE the problem into an equation.
3. SOLVE the equation.
4 INTERPRET the results Check the proposed
solution in the stated problem and state
your conclusion. |

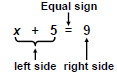
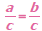

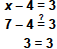
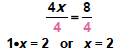
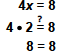
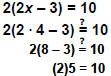
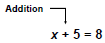
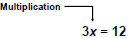
 Read and reread the problem.
Read and reread the problem.