REVIEW WORKSHEET FOR MTH 1030

PART I (NO PARTIAL CREDIT, NO CALCULATORS ALLOWED ).
ON THE FINAL EXAM, THERE WILL BE 25 MULTIPLE CHOICE QUESTIONS ON THIS PART, WITH PROBLEMS SIMILAR TO OR SLIGHTLY DIFFERENT FROM ANY OF THE FOLLOWING:

1. Find the distance between the points (-4, -7) and (6, -1)

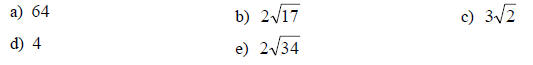
2. Simplify: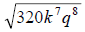

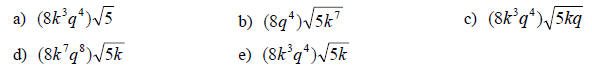
3. Simplify: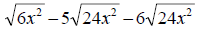

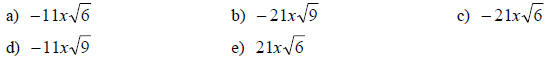
4. Simplify: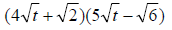

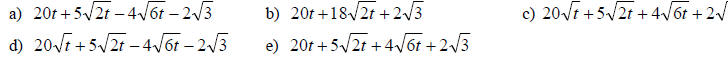
5. Simplify: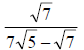

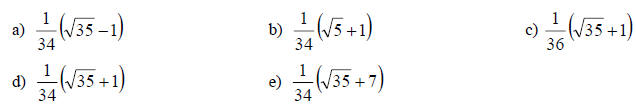
6. Simplify: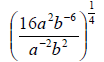

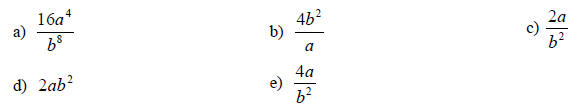
7. Simplify: (9 + 2i)(6 - 7i)

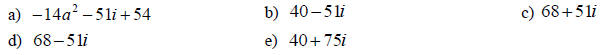
8. Simplify: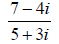

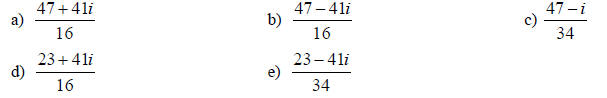
9. Solve for x: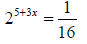

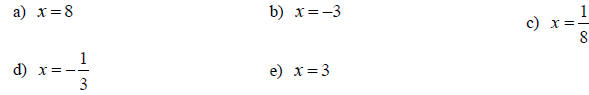
10. Solve for x: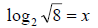

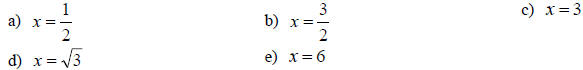
11. Use the properties of logarithms to rewrite :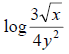

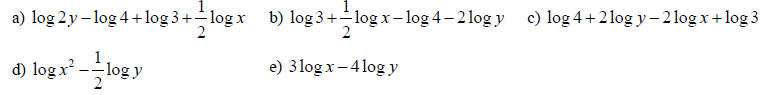
12. The equation of the circle of radius 4 with center (-2, 4) is:

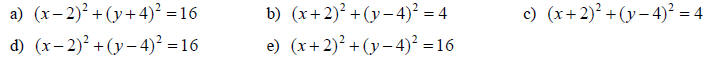
13. Simplify: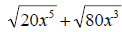

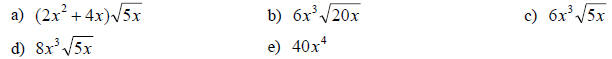
14. The vertex (turning point) of the parabola y - x² = 4x - 6 is:

15. Find x in the triangle below:

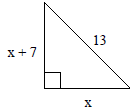
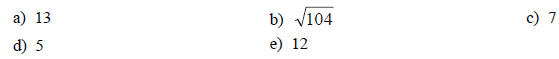
16. Simplify: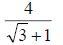

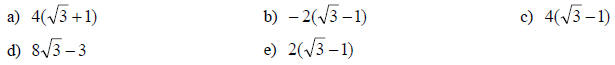
17. Evaluate: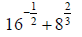

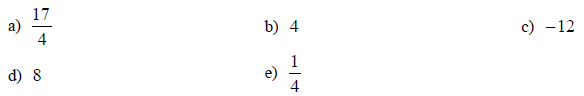
18. Add and simplify :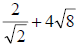

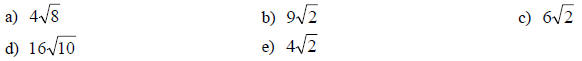
19. Express in the form a + bi: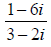

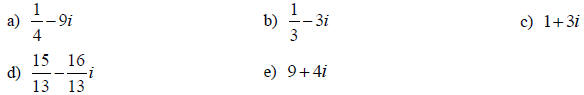
20. Compute: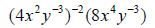

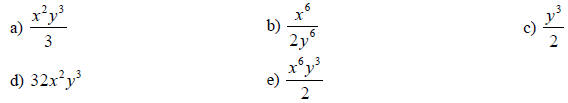
21. Find x in the triangle below:

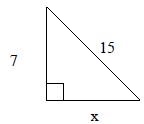
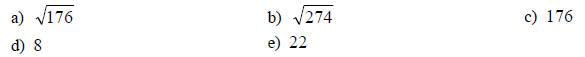
22. If f(x) = 2x² - x + 6, find : f(-3):

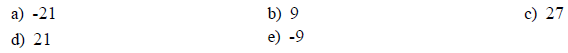
23. What is the discriminant of ? y = 2x² - 4x - 3 ?

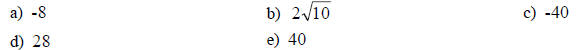
24. Simplify: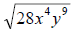

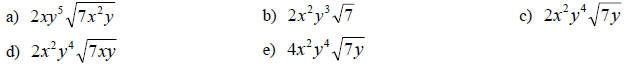
25. Find the center and radius of the circle: x² + y² + 5x - 6y - 2 = 0

26. Write in terms of rlogr ,logs,logt:

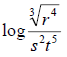
27. Solve the system of equations:

28. Solve for x: log(2 + x) + log(x - 3) = log14

29. Find the solution set of the inequality : t² - 2t - 3 ≤ 0

30. Solve the inequality: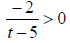

31. Solve for x: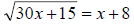

32. Solve for x: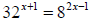

33. Given: y = x² - 4x - 5
a) Find the y- intercept .
b) Find the x-intercept(s).
c) Find the coordinates of the vertex.
d) Sketch the graph.

34. Rationalize and evaluate when h = 0: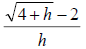

35. Solve for x:
a) x² + 8x + 9 = 0 (You must use completing the square method.)
b) 5x² + x = -2 (You must use the quadratic formula method.)

36. Solve the system of equations:

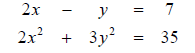
37. Solve for x: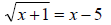

38. Solve for x: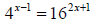

39. Solve for x: 2x² + x + 2 = 0

40. Solve for x: 2x² + 3x - 2 = 0

41. Solve for x: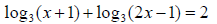

42. Simplify, leaving no negative exponents :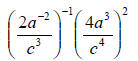

43. Given: y = x² - 2x - 3
a) Find the y-intercept.
b) Find the x-intercept(s).
c) Find the coordinates of the vertex.
d) Sketch the graph.

44. Find the center and radius of the circle given by the following equation:

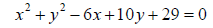
45. Simplify: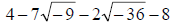

46. Rationalize and evaluate when h = 0: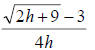

47. Solve the inequality: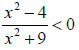

48. Solve the system of equations:

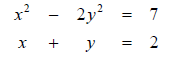
49. Express as a single log term: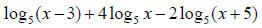

50. Solve for x: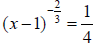

51. Solve for x: x^-2 - x^-1 = 12

52. Find the inverse of f(x) = 4x - 3

53. Solve for x: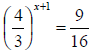

54. Determine the solution set (inequality): x² - 6x - 27 > 0

55. Given:

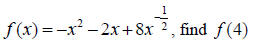
56. Simplify and express the answer without negative exponents:

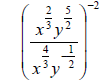
57. Solve the inequality: 2x² + 5x - 3 ≥ 0

58. Completely simplify to a single fraction :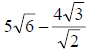

PART II (CALCULATOR ALLOWED).
THIS PART OF THE FINAL EXAM WILL HAVE 10 MULTIPLE CHOICE QUESTIONS.
THE FORMAT OF THE ANSWER CHOICES WILL BE SIMILAR TO THOSE ON THE ANSWER SHEET FOR THIS REVIEW.

59. Given the equation of the circle x² + y² = 169 at the point A (12, -5):
a) Find the equation of the line tangent to the circle at point A.
b) Find the value of y (to the nearest hundredth) on the tangent line at point A if x = 12.01.
c) Find the value of y on the circle if x = 12.01.

60. If $7500 is deposited in a bank paying interest at an annual rate of 8% compounded continuously , how much will be in the account after 3 years and 9 months? (Assume no withdrawals are made.)

61. Determine the equation of the tangent line to x² + y² = 25 at the point (-3, 4) and compare the y-values on the tangent line to the curve when x = -2.98.

62. If $4000 is invested for 2 years (compounded annually) and grows to $4326, approximately
what annual rate did the money earn?

63. Given the profit function, p(x) = -2x² + 240x - 6400 where x is the number of items produced and sold:
a) Find the number of items to be produced and sold when break-even occurs (profit = 0).
b) Find the # of items (produced and sold) that will maximize the profit.
c) Find the amount of maximum profit.

64. Assume that you deposit $1,000 at 8% compounded annually. How long will it take for your money to be tripled?

65. Solve for x: 6^x-1 = 201.

66. Assume that sales of a product in year n is given by the formula S = 1000e^-0.051(n-2). To the
nearest cent, what are the sales in year 15?

67. Solve for x: 43x² - 52x = 14

68. Determine to the nearest thousandth: log₉216

69. Find the distance between the points (5, -16), (-19, -22) [Round your answer to 2 decimal places .]