Rational Expressions and Applications

Chapter 6: Rational Expressions and Applications
• Algebraic Fractions ; simplification and solving
• Finding common denominators and Least Common Denominators
• Multiplication, Division, Addition and Subtraction
• Applications

Section 6.1: The Fundamental Property of rational Expressions
• We first define a rational expression then look at procedures used to simplify the expression.
• Factoring techniques will be used (Chapter 5)

Rational Expressions: A rational expression, or algebraic, fraction is the quotient of two polynomials with the denominator not equal to zero.

• We cannot divide by zero ; division by zero is undefined
• It is necessary to determine, for what values of x, the denominator is zero

Steps to Determining When a Rational Expression is Undefined
1. Set the denominator equal to zero
2. Solve the resulting equation
3. The solution (s) is the value(s) for which the rational expression is undefined

Examples: Find the values that make the rational expression undefined

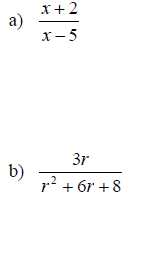
Writing Rational Expressions in Lowest Terms
• A rational expression is in lowest terms if the greatest common factor of the numerator and denominator is 1

Steps
1. Factor the numerator and denominator completely; write numbers in their prime powers
2. Divide out any common factors using the idea that a/a=1

Examples: Write each rational expression in lowest terms

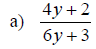
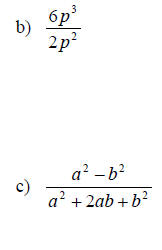
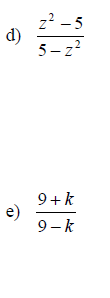
Section 6.2: Multiplying and Dividing Rational Expressions
• When multiplying rational expressions we multiply the numerators together and the denominators together
• When dividing rational expressions we multiply the first fraction by the reciprocal of the second fraction
• Before performing the multiplication or division, write each rational expression in lowest terms
• Once the multiplication or division has been completed, write the final rational expression in lowest terms

Examples: Perform the indicated operation. Write the final result in lowest terms.

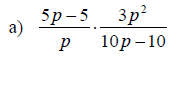
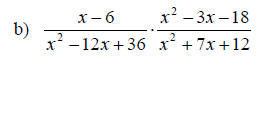
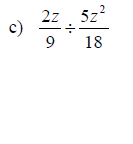
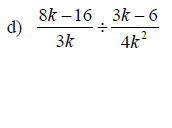
Section 6.3: Least Common Denominators
• When adding or subtracting rational expression a common denominator must be used
• The LCD is the simplest expression that is divisible by all the denominators in the rational expression
• This section introduces how to find the LCD
• In section 6.4 we will use the LCD to add and subtract rational expressions

Finding the Least Common Denominator
1. Factor each denominator into prime factors
2. List each of the different denominator factors the greatest number of times it appears in any of the denominators
3. Multiply the factors found in step 2

Examples: Find the LCD for each group of fractions given

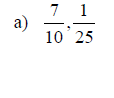
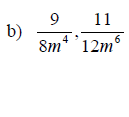
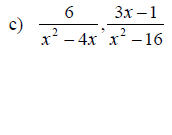
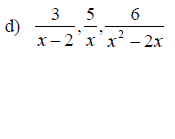
Writing a Rational Expression with a Specified Denominator
1. Factor both denominators
2. Decide what factor(s) the denominator must be multiplied by in order to equal the specified denominator
3. Multiply the rational expression by that factor divided by itself; multiply by 1

Examples: Rewrite the rational expression with the indicated denominator

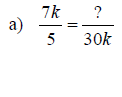
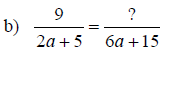
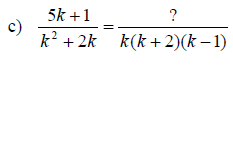
Section 6.4: Adding and Subtracting Rational Expressions
• When adding or subtracting rational expressions a common denominator is used
• If the expressions already have a common denominator then combine the numerators under the single denominator
• If the expressions do not have the same denominator, we use the LCD method as discussed in Section 6.3

Steps for Adding/Subtracting Rational Expression with Different Denominators
1. Find the LCD
2. Rewrite the rational expression as an equivalent rational expression with the LCD as the denominator
3. Combine the numerators under the single denominator
4. Write the resulting expression in lowest terms

Note: Addition or Subtraction cannot be performed unless the denominators are the same!

Examples: Add or Subtract. Write the final result in lowest terms

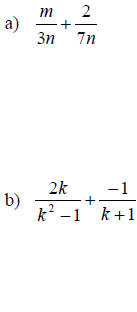
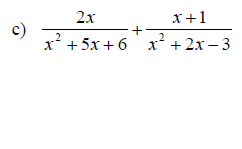
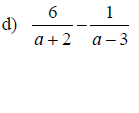
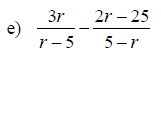
Section 6.5: Complex Fractions
• A complex fraction is a rational expression with one or more fractions in the numerator, or denominator, or both

Steps to Simplify Complex Fractions
1. Write both the numerator and the denominator as a single fraction in lowest terms
2. Rewrite the complex fraction as a division problem
3. Perform the division of rational expressions by multiplying by the reciprocal
4. Write the final result in lowest terms

Examples: Simplify each complex fraction

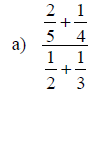
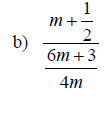
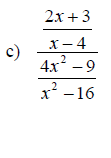
Section 6.6: Solving Equations with Rational Expressions
• In this section we make the distinction between expressions and equations
• Expressions can be simplified
• Equations have an equal sign and can be solved

Use of the LCD in Simplifying and Solving
• When simplifying, adding or subtracting, get a LCD and simplify the numerators
• When solving rational equations, get a LCD so as to eliminate the denominators and solve the resulting equation in the numerators

Examples: Solve the given rational equations. Check the solution.

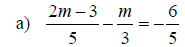
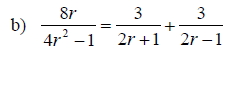
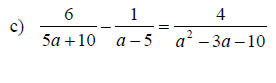
Solving Equations for a Specified Variable
• Treat the variable that is being solved for as the only variable and all other variables as constants.

Examples: Solve the equation for the specified variable. Write the result as a single fraction.

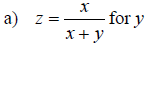
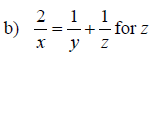
Section 6.7: Applications of Rational Expressions
• When solving application problems we can apply the 6 Step Method

Problem Solving Steps
1. Read the problem carefully
2. Assign the variable
3. Write an equation
4. Solve the equation
5. State the answer
6. Check the solution

Examples: Solve the following application problems using the 6 step method described previously.
1. At the 2006 Winter Olympics, Joey Cheek of the United States won the 500-m speed skating event for men in 69.76 sec. What was his rate (to the nearest hundredth)?

2. A boat can go 10 mi against the current in the same time it can 30 mi with the current. The current has a flow of 4 mph. Find the speed of the boat.

3. Al and Mario operate a small house cleaning company. Mario can clean an average house alone in 3hrs. Al can clean a house alone in 5hrs. How long will it take them to do the job if they work together?