Polynomials

Factoring
The process of factoring is a type of ”reverse-multiplication”, where you are given a polynomial and have to
write it as a product of factors. A polynomial is completely factored when each factor is prime, or cannot be
factored again. The idea is very similar to factoring numbers: 60 =5 ·12 is
one factoring of 60

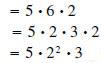
is the prime factorization of 60
There are several strategies to determine how to factor polynomials.

I. Common Factors

A common factor is a factor of every term of an expression . Common factors can be pulled out of an
expression using the distributive property in reverse :

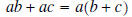
Examples:

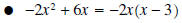(Note the negative in the second term)

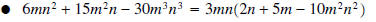
Finding common factors should always be the first step in factoring an expression.

II. Factoring by Grouping

Factoring by Grouping is especially useful when you have more than three terms in the polynomial. The
technique of factoring by grouping is really using common factors creatively, as shown in the following
example:

Example 1: Factor 2x³ - x² + 6x - 3
Solution : Although there is no factor common to all terms (except 1, which we ignore), we can ”group”
the polynomial by twos, each of which have a common factor:

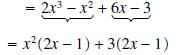
Now notice that there are two terms , each of which has the factor 2x - 1.

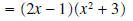
It is very easy to check your answer by mulitplying it out:

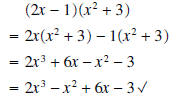
III. Factoring Using Special Products

The special products we learned in the section ”Products of Polynomials” can be used to help factor
expressions which have an appropriate form:

Example 2: Factor completely x³ - 9x
Solution: As mentioned in the previous section, the first thing we do is look for a common factor:

Notice how the second factor can now be written as x² - 3² , a difference of two squares. Recall that

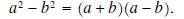
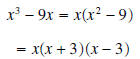
The expression is now completely factored.

Example 3: Factor completely x³ + 8y³
Solution: Notice how the expression can be rewritten as (x) ³ + (2y) ³, a sum of two cubes. Recall that

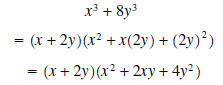
Example 4: Factor completely x² + 25
Solution: Recall that there is no special product for a sum of squares a² + b² . In fact, this expression
cannot be factored; it is prime over the real numbers.

IV. Factoring Binomials (x² + bx+ c )

If possible, a binomial of this form must factor as (x + m)(x + n) , where m and n are integers. Note that if this
is true:

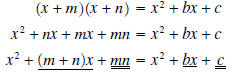
We can see in the last statement that the numbers m and n that we seek must add up to b and multiply to c.

Example 5: Factor completely x² + 7x + 12
Solution: We are looking for two numbers which will add up to 7 and multiply to 12. The numbers
(obtained by trial and error) are 3 and 4. Therefore,

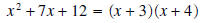
Example 6: Factor completely x² - 4x - 21
Solution: We are looking for two numbers which will add up to -3 and multiply to -21. Note that since
the product is negative , the numbers must be different signs (one negative and one positive). The numbers are
-7 and 3 (Note that if we had chosen 7 and -3, the numbers add up to +4. In general, if the signs are
different , the larger number will have the same sign as b, the middle term). Therefore,

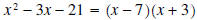
Example 7: Factor completely x² - 6x + 9
Solution: We are looking for two numbers which will add up to -6 and multiply to 9. Note that since
the product is positive, the numbers must be the same sign (both positive or both negative). Since the middle
term is negative, the numbers must both be negative. The numbers are -3 and -3. Therefor

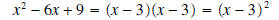
Note that we could have factored this using the special product ( a- b) ²= a² - 2ab + b²

V. Factoring Trinomials (ax² + bx + c )

If possible, a trinomial of this form (where the leading coefficient is not 1) must factor in the form
(mx + s)(nx + t) , where m, n, s, and t are all integers. It is possible to find these numbers by trial and error;
however, such a method may at times be haphazard or tedious. The following is a more straightforward
approach utilizing the technique of factoring by grouping.

First, we need to split the middle term bx into two terms which will allow us to factor by grouping. To do this,
we use a similar technique as before, only now we look for two numbers whose sum is b and whose product is
ac .
If you are curious as to why, see below:
As before, multiply the desired form out:

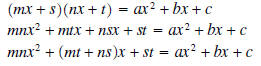
Now note that b = mt + ns and ac = (mn) (st) = (mt) (ns) . The numbers we are
looking for are mt and ns. How they split up into m,n, s, and t are determined when we
factor by grouping.

Example 8: Factor completely 9x² - 3x - 2
Solution: We first must find two numbers whose sum is -3 and whose product is (9)(-2) = (-18). The
numbers are -6 and 3. Now we rewrite -3x as - 6x + 3x and factor by grouping:

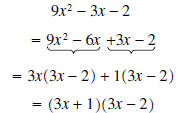
(remember that you can check your answer by multiplying)

Example 9: Factor completely 6x² - x - 15
Solution: We must first find two numbers whose sum is -1 and whose product is (6) (-15) = -90. The
numbers are 9 and -10. Now we rewrite -x as 9x 1-0x and factor by grouping:

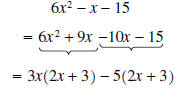
(Notice that both signs change in the last term)

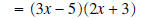
If you are afraid of getting the middle terms in the wrong order , not to worry...

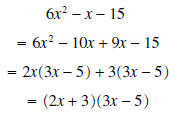
the same as above.