Polynomial Functions
Textbook pages 21-24
(i) Definition and Examples:
Definition:
Examples:
•
•
•
•
(ii) Quadratic functions = Second order polynomial
The general expression for a quadratic function is
The graph of a quadratic function is a parabola. The most common example is the
function
f(x) = x2:
Examples of parabola in Nature :
The trajectory of objects thrown
• from a height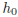 
(in meters)
• at velocity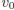
(in meters/second)
• at an angle α
is given by the function
where g = 9.8 m/s2 is the constant of gravitational
acceleration.
Example of the lucky kid shot! At what velocity is he throwing the ball?
• Height of a basketball hoop: 3.05 meters
• Angle of throw: 30°
• Length of court: 28.65 meters
(iii) Manipulating Quadratics
There are two typical questions one may ask:
• Type A: What is the relationship between the coefficients a , b and c and the
charac-
teristics of the graph of a parabola (position and height of the
minimum/maximum,
position of the zeros).
• Type B: Given an equation ax 2 + bx + c = 0, can we find x?
These questions are illustrated in this diagram:
Type A questions: To answer this question, we must
complete the square in the expression
f(x) = ax2 + bx + c:
That’s in the form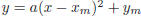 
with
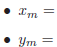
Graphically, this can be interpreted as the following scaling operations on the
standard
parabola:
Type B questions: To answer this question, we start from
the result of the previous
question, and keep manipulating the expression:
so that the equation ax2 + bx + c = 0 becomes
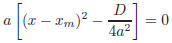with
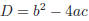
We see that
• if D < 0 then
• if D = 0 then
• if D > 0 then
Examples:
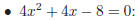
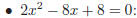
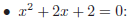
(iv) Factoring polynomials
Definition:
In practise: For quadratic polynomials f (x) = ax2 + bx + c
• Calculate D = b2− 4ac
• Identify how many solutions there are, and what they are
• If D < 0 there are no solutions, then f(x) cannot be factored
• If D = 0 there is one solutio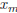n 
then
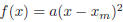
• If D > 0 there are two solutions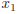 
and
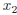then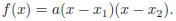 
Examples:
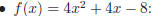
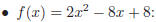
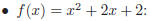
Note: Factoring higher order polynomials is more difficult
since there exist no general
method for finding roots . However, if you know a root (for example if the root
is obvious, or
if it given to you in the problem), you can factor the polynomial using long
division .
Example: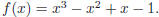 
(v) Signs Tables
Signs Tables are an excellent tool to determine the sign of a polynomial
function. In or-
der to use signs tables, the function must already be broken down into its
factors. Then
• Draw the table
• Write all the factors vertically on the left
• Write all the roots horizontally on the top (in the correct order)
• Draw vertical lines below each root
• Determine and write the sign of each factor; write zeros where appropriate.
• Multiply the signs in each interval to determine the sign of the function.
Example: f(x) = 4(x − 1)(x + 2).
Example: f(x) = (x − 1)(x2 + 1).
Example: f(x) = (x − 2)(x + 1)(x2− 3).
Check your understanding of Lecture 2
• The order of a polynomial:
What is the order of the following polynomials: f(x) = x4, f(x) = 2, f(x) = (x −
2)7,
f(x) = (x + 2)(x2 + 1).
• For each of the following polynomials: (1) find the roots when they exist. (2)
write the
polynomial in factorised form. (3) draw and complete the corresponding signs
table to
identify where f(x) > 0 and f(x) < 0.
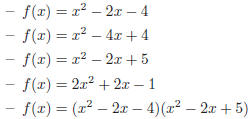
• For the first 3 polynomials of the previous question,
determine the coordinates
of their maximum/minimum, and using all of the information you have, sketch them
on a graph.
| Prev | Next |