Outline of material in Chapters 1 and 2

1.1 – Four ways to represent a function
Examples of functions
Definition of function
Domain, range, in/dependent variable
Ways to picture a function: machine, arrow diagram, graph
4 ways to represent a function:
Verbally (description)
Numerically (table)
Visually (graph)
Algebraically (formula)
Vertical Line Test for a curve to be the graph of a function
Piecewise defined functions
Absolute value function
Even & odd functions
Increasing & decreasing functions

1.2 – Mathematical models: a catalog of essential functions
Mathematical model
Linear function
Polynomial ( terms : degree, coefficients , quadratic , cubic)
Power function and its graph
Rational function
Algebraic function
Trigonometric function
Exponential function and its graph
Logarithmic function and its graph
Transcendental function

1.3 – New functions from old functions
Transformations
Vertical & horizontal shifts
Vertical & horizontal stretching & reflecting
Combinations
f +-×÷ g
f ○ g : Composition of functions

1.4 – Graphing Calculators
Viewing rectangle

1.5 – Exponential functions
Define and graph a^x for all positive real numbers a
Cases for a : a>1, 0<a<1, a=1
Laws of exponents
Application to population models
The number e

1.6 – Inverse functions and logarithms
One-to-one function
Horizontal line test
Definition of inverse function of a one-to-one function (Example 4)
Domain and range of inverse function
“Cancellation” equations
Finding the inverse of a one-to-one function
Relation between graph of f^-1 and that of f
Logarithm: the inverse of the exponential function
Laws of Logarithms
Natural Logarithms
Change of Base formula
Inverse Trig. functions

2.1 – Tangent and velocity problems
Motivating the idea of the derivative (not yet mentioned by name) as a limit:
Slope of tangent line as limit of slopes of secant lines
Instantaneous velocity as limit of average velocities

2.2 – The limit of a function
Definition of limit
Guessing limits from a sequence of evaluations
One-sided limits
Limit exists if & only if the two one -sided limits exist and are equal

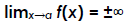
Vertical asymptote

2.3 – Calculating limits using the limit laws
Basic five Limit Laws
Additional Limit Laws #6-11
Direct Substitution Property for polynomial & rational functions (holds for all continuous functions)
Limit exists if & only if the two one-sided limits exist and are equal (repeated from 2.2)
Using the above to calculate limits using one-sided limits, e.g., involving absolute value
Squeeze Theorem

2.5 – Continuity
Definition only

2.6 – Limits at infinity; horizontal asymptotes

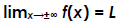
Horizontal asymptote
Calculating 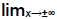of a rational function using 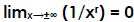(Example 3)
Examples of 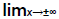with square roots (Examples 4&5)
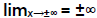(Examples 8-11)
(Skip Precise Definitions subsection)

2.7 – Derivatives
Slope of tangent line, revisited – express as a limit that we now can calculate
Same for instantaneous velocity
The mathematics of these two examples is the same, leading to
Definition of the Derivative (two forms: with h and with a)
Finding equation of tangent line to curve y=f(x) at point ( a, f(a) ) (Example 5)
More general interpretation of the derivative:
rate of change of one variable with respect to another (Example 6)

2.8 – The derivative as a function
Not on Test #1; on next test.