math homework

1. (1.4) (a) n = 1, 1 = 1. n = 2, 1 + 3 = 4. n = 3, 1 + 3 + 5 = 9. n = 4,
1 + 3 + 5 + 7 = 16. Our guess is 1 + 3 + … + (2n - 1) = n^2

(b) Prove that 1 + 3 +  … + (2n - 1) = n^2 for every n ∈ N.

Proof: Let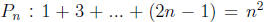be the nth proposition.

We check the basis for induction P1 is true since P₁ : 1 = 1^2. For the
induction step , assume that P_n is true. We want to prove P_n+1 is true.
To verify it we write:

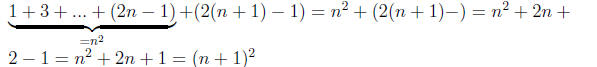
Thus P_n+1 is true. By mathematical induction P_n is true for every n ∈ N.

2. (1.6) Prove that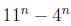is divisible by 7 when n ∈ N

Proof: Let P_n : 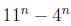is divisible by 7, be the nth proposition. We
check the basis for induction P1 is true since:

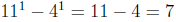which is divisible by 7.

For the induction step, we assume that P_n is true. We want to prove that P_n+1 is true.

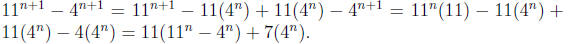
By hypothesis of induction 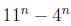is divisible by 7, in other words 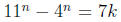for some integer k.
Then we have that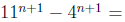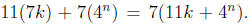Thus P_n+1 is true. Applying mathematical
induction we have that P_n is true for every natural number n.

3. (1.9) see the back of the book

4. (2.4) Setting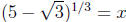we find that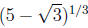is a solution for
the polynomial equation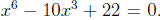If there were a rational
solution r = p/q for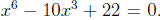then the Rational Zeros
Theorem would imply that p divides 22 and q divides 1.We would
have that 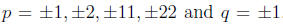Thus the only possible
rational solutions for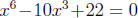 would be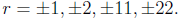
But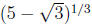is a solution and it is not equal to any of the possible
values for r . Therefore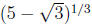is not a rational number .

5. (2.6) If b rational then 4-7b^2 is rational.

Proof: b is rational then b = p/q for some p, q ∈ Z and q ≠ 0. We
wanto to prove that 4-7b^2 is rational. We write;

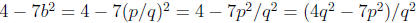
The top and bottom parts are integers. ( We know that integers are
closed under multiplication and sum ). Also q^2 ≠ 0. Thus 4-7b^2 is a
rational number .

6. (1.12) (a) you can do it!
(b) Show that

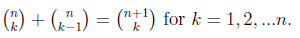
Proof: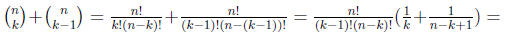

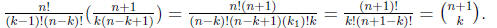
(c) Prove the binomial theorem using mathematical induction and part

(b) Proof: Let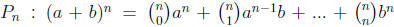be
the nth statement. We check the basis of induction P₁ is true, since
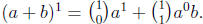For the induction step we assume that P_n is
true. We want to prove that P_n+1 is true.

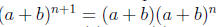(By hypothesis of induction we can write)
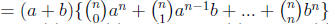(using distributive law )

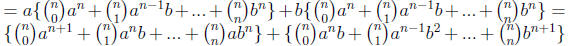
(we associate the terms containing the same aⁱb^j)

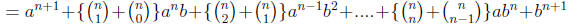
Now we use part (b)

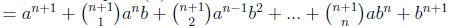
This proves that P_n+1 is true

7. Try: Indicate what is wrong in the following "proof". This problem is known as Polya's Paradox.

Theorem: For each n ∈ N, let P(n) be the statement "Any collection
of n marbles consists of marbles of the same color." Then P(n) is true
for all n ∈ N.

Proof: Clearly, P(1) is a true statement. Now suppose that P(k) is a
true statement for some k ∈ N. Let S be a collection of k+1 marbles. If
one marble, call it x, is removed , then the induction hypothesis applied
to the remaining k marbles implies that these k marbles all have the
same color. Call this color C . Now if x is returned to the set S and a
different marble is removed, then again the remaining k marbles must
all be of the same color C . But one of these marbles is x, so in fact
all k + 1 marbles have the same color C . Thus P(k + 1) is true, and
by induction we conclude that P(n) is true for all n ∈ N.

Solution: If n = 2, then the two sets dont overlap. This paradox is
meant to illustrate that sometimes there are special cases that must be
proved separately, like n = 2 here. Since we cannot prove all pairs of
horses have the same color, the proof does not work (as it shouldnt,
because the claim that all horses are the same color is false!).