Math 8 Exam 1 Solutions
You will not receive full credit if you do not clearly
show work as demonstrated
in class. Show all work in the space provided on this exam. Circle your answers .
|
1. Add , subtract, or multiply as directed. Express your answer as a single polynomial in standard form. |
(16 points) |
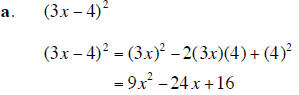
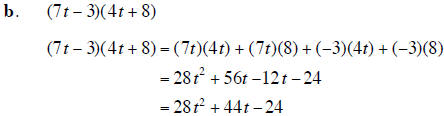
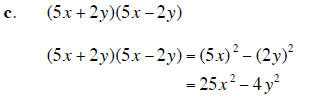
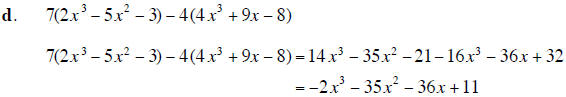
| 2. Use synthetic division to find the quotient and
remainder when
2x4 − 3x2 + 2 is divided by x − 2. |
(5 points) |
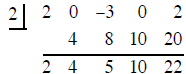
So the quotient is 2x3 + 4 x2 + 5x +10 and the remainder is 22.
3. Simplify each expression . Assume that all variables are positive when they appear. (15 points)
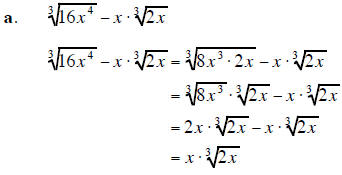
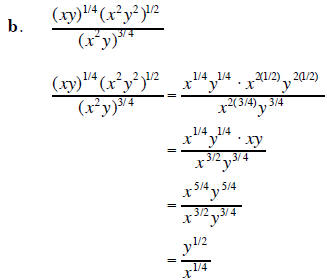
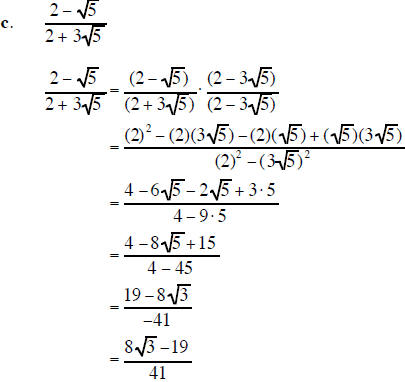
4. Factor completely each polynomial. If the polynomial cannot be factored, say it is prime. (20 points)
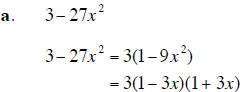
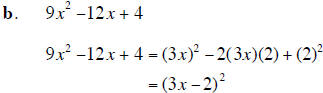
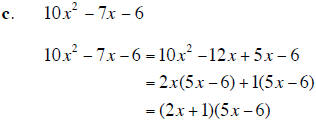
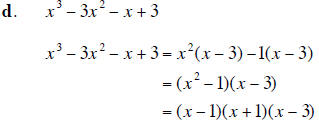
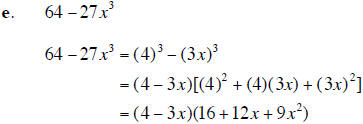
5. Use synthetic division to determine whether x + 4 is a factor of x6 −16x4 + x2 −16 . (5 points)
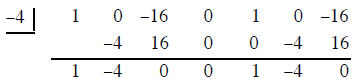
Since the remainder is zero , x + 4 is a factor of x6 −16x4 + x2 −16
|
6. Perform the indicated operation and simplify the result. Leave your answer in factored form . |
(20 points) |
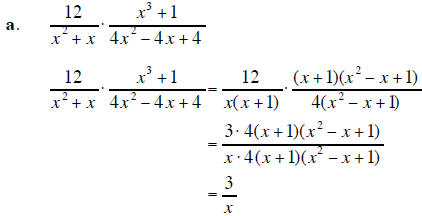
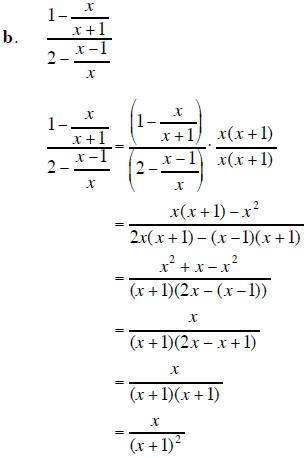
6. Continued from the previous page .
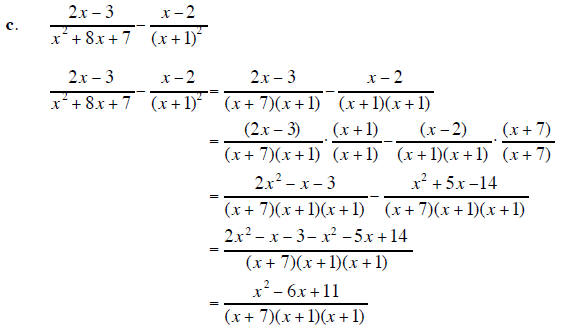
7. Find the quotient and remainder when 2x4 − 3x3 + x +1 is divided by 2x2 + x +1. (5 points)
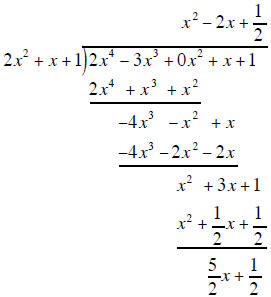
So the quotient is 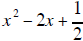 and
the remainder is
and
the remainder is 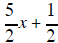 .
.
| 8. Simplify each expression . | (10 points) |
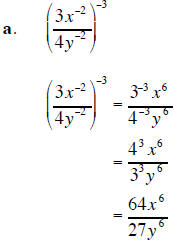
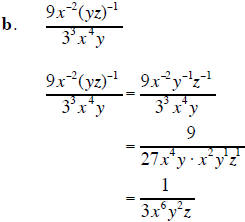
9. Find the value of 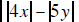 when x = 3 and y = −2.
when x = 3 and y = −2. |
(4 points) |
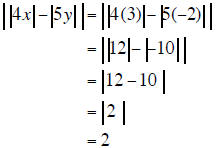
| Prev | Next |