LEONHARD EULER
Pell's equation
Before I begin, I observe that Euler does use the term
Pell's equation and
that following him the term passed into general use, but that the equation
itself was introduced by Fermat in 1657 as a problem to mathematicians in
general and to several English mathematicians in particular. It was solved
within little more than a year by Fermat himself and by the English
mathematicians.
If n is an integer and not 0, it is not possible for n2 +
1 to be a square
of a rational number , for that rational number would - if taken positive -
have to be an integer larger than n, thus of the form n + m and (n + m)2 =
n2 +2mn+m2 is certainly larger than n2 + 1 because 2mn and m2 are both
at least 1. On the other hand it might be possible for an2 +1 to be a square,
not of course if a is negative or itself a square, but otherwise. This is the
question investigated by Euler in Chapter 7 of II.2.
He begins his investigation with the following remark, in
which one sees
the name Pell mistakenly appearing.
"Hiezu hat ein gelehrter Engl¨ander, Namens Pell, eine
sehr sinnreiche Methode
erfunden, welche wir hier erkl¨aren wollen. Dieselbe ist nicht so bescha en,
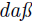sie auf allgemeine Art
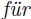jede Zahl a, sondern nur
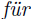jeden besondern
Fall gebraucht werden kann."
The last remark is more important to us than the reference
to Pell. The
method is a general method, but as a number-theoretic method and not an
algebraic method ; it is applied to an individual equation to obtain an answer.
There is no general algebraic formula .
Suppose we want to 2n2 + 1 to be the square. If it is the
square of some
number, that number can be taken to be positive and it will necessarily be
larger than n. Write it as n + p. Then
2n2 + 1 = n2 + 2pn + p2
n2
= 2np + p2 − 1.
This is a quadratic equation for n that can be solved to give
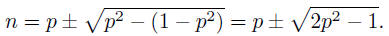
This number is only good to us if 2p2−1 is a square. One
possibility is p = 1.
This leads to n = 0, which is uninteresting or n = 2 and then
2n2 +1 = 9 = 32.
This example was so easy, although we applied the general
method, that
we try another, again taken from Euler's Algebra. We want to find an integral
solution of 13n2+1 = m2. One possibility is n = 0, m = 1, but we are looking
for solutions of more interest.
Since 9n2 < m2 < 16n2, we conclude that m = 3n + p with
p < n, so
that
13n2 + 1 = 9n2 + 6np + p2
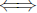4n2 − 6pn − p2 + 1 = 0.
Thus
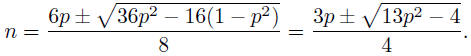
We have to chose the +- sign . It is clear from this that n
> 6p/4 and that
n < 7p/4 so that 2p > n > p and therefore n = p + q, with q < p.
Continuing, we see that
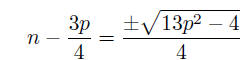
or
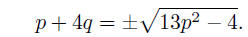
Squaring, we obtain
p2 + 8pq + 16q2 = 13p2 − 4
12p2 − 8pq − 16q2 − 4 = 0.
The last equation can be divided by 4; the result is
3p2 − 2pq − 4q2 − 1 = 0.
We could decide to give these calculations up , fearing
that they would
continue forever, except that q is positive and smaller than p which is in turn
smaller than n. Since these numbers are growing smaller and smaller, we will
be forced to stop sooner or later. So we continue.
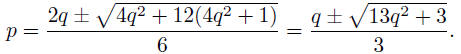
We might be tempted to try q = 1 here, so that p = (q
± 4q)/4. With either
sign, p is not integral, so that we have to continue.
Once again, we have to take the positive root if p is to
be larger than q.
Then 5q/4 > p > 4q/4, so that p = q + r with r < q. Thus q = r + s with
s < r. We continue and we now continue more rapidly, observing that we
have at each stage to take the positive square root.
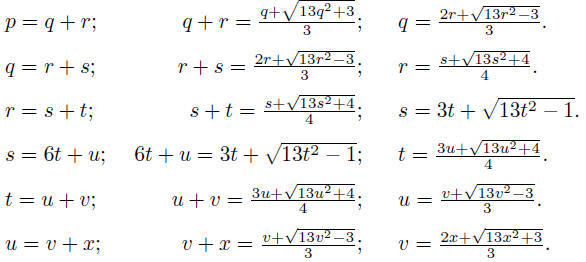
At this point, we can observe that x = 1 makes 13x2 +3 a
square and that it
makes v integral, namely v = 2. Euler takes the process two steps further . If
v = 2 then
u = v + x = 3,
t = u + v = 5,
s = 6t + u = 33,
r = s + t = 33+5 = 38,
q = r + s = 38+33 = 71,
p = q + r = 71 + 38 = 109,
n = p + q = 109 + 71 = 180,
m = 3n + p = 540 + 109 = 649.
Thus
13n2 + 1 = 421201 = 6492.
We could perhaps take x larger, but not smaller, since x =
0 does not make
13x2 + 3 a square. In other words, we may very well not have found all
solutions. This is indeed so. It is worth while to look more carefully at these
calculations and to see how we might find others.
We continue Euler's calculations. He writes
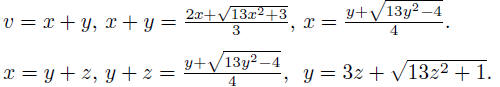
At this point, we are free to take the trivial solution
that we earlier rejected,
namely z = 0, which yields y = 1 and then x = 1 as before.
This leads, as we know, to the solution n = 180, m = 649,
but now we
can start with this value of n , taking it for z. This gives the following
results.
y = 1189,
x = y + z = 1189 + 180 = 1369,
v = x + y = 1369 + 1189 = 2558,
u = v + x = 2558 + 1369 = 3927,
t = u + v = 3927 + 2558 = 6485,
s = 6t + u = 6 × 6485 + 3927 = 42837,
r = s + t = 42837 + 6485 = 49322,
q = r + s = 49322 + 42837 = 92159,
p = q + r = 92159 + 49322 = 141481,
n = p + q = 141481 + 92159 = 233640,
m = 3n + p = 3 × 233640 + 141481 = 842401.
Then
13n2 + 1 = 709639444801 = m2.
So we have found another solution. We could continue!
Before returning to Fermat's equation, I pass to Euler's
next chapter,
which is entitled Von der Art, wie die Irrationalformel
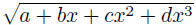
rational gemacht wird. In other words, he wants to find solutions of the
equation
| Prev | Next |