INTRODUCTION TO DECIMALS

In this section, we will explore relationships between fractions and decimals and see how decimals
are an extension of the base-ten number system . The word decimal comes from the Latin decem,
meaning “ten”.

RELATING TO MONEY
One of everyone’s first encounters with a decimal is in the context of money. A child sees the
price of an IPOD Shuffle is $79.84. Let’s look at different ways to express this money amount.

$79.84 = “______________________________________________________” (words)
$79.84 = ______________________ Because $0.84 is __________________of a dollar.
$79.84 = __________ dollars + __________ dimes + __________ pennies

__________ + _______ . ____________ + _____________ . _______________
Because a dime is _____________ of a dollar and a penny is _________________ of a dollar.

EXPANDED NOTATION

$79.84 = __________ + __________ + ________ . _________ + ____________ . ________________
= _____________ + _____________ + _____________ + _____________

READ THE FOLLOWING NUMBERS. THEN WRITE IN EXPANDED NOTATION USING
POWERS OF 10.

12.659 = _____________________________________________________________
409.0783 = _____________________________________________________________
0.54321 = _____________________________________________________________
2,084.08 = _____________________________________________________________

CONCRETE REPRESENTATIONS
We can use Base-10 blocks to help model decimals. However, we might need to change what each
block represents from problem to problem. The unit block should always represent the “smallest
place” in the number. Draw the Base -10 block representation of each.

CONVERTING FRACTIONS TO DECIMALS

1. DENOMINATOR IS A POWER OF 10
Read the fraction and write as a decimal.

2. DENOMINATOR IS NOT A POWER OF 10
If the denominator is not a power of 10, as in 3/5, we can convert it so it does.
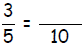which is ________ (as a decimal)

Before we take this further, let’s look at the powers of 10 and see what they have in
common . Write the prime factorization of each of the following:

10
100
1,000
10,000

What do we see in common?

How is the exponent (s) related to the number of zeros in the original number?

Using what we just concluded above, we can easily change the following fractions to decimals.

Notice that in all the above examples we were able to change the denominator to some power of
10. The original denominators were all combinations of 2’s and/or 5’s and we simply incorporated
in through multiplication enough 2’s or 5’s to make a power of 10. They are all examples of
terminating decimals – decimals that can be written with a finite number of places to the
right of the decimal point.
But what about: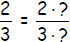
What can we multiply 3 by to get a power of 10?
(This is an example of a decimal that does not terminate.)

The leads us to the following theorem:

NOTE: To determine whether a rational number can be represented as a terminating
decimal, we only need to consider the prime factorization of the denominator, BUT
The fraction must be in simplest (reduced) form first.
Which of the following can be written as a terminating decimal? Explain why or why not.

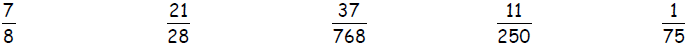
ORDERING TERMINATING DECIMALS
1. Line up the numbers by place value
2. Start at the left and find where the digits differ
3. Compare these digits. The number with the larger digit is greater
4. NEGATIVES ARE IN REVERSE

0.543 _______ 0.563 2.765 _______ 3.765 0.0087 _______ 0.087

-2.34 _______ -2.35 43.566 _______ 34.566

Order from greatest to least :

3.45
3.35
3.42
3.451
3.358
3.405