Homework on rational numbers

Since this is homework, you should complete this worksheet individually. As usual with home-
work, I don’t mind if you share ideas with each other, but you copying each other’s work is cheating.
So don’t!

We have talked about the rational numbers in class and have reviewed rational arithmetic in
class along with the reasons for it. In this worksheet, you will investigate some properties of the
rational numbers.

First, recall the

Definition. A rational number is a number of the form m/n where m and n are integers and
n ≠ 0.

As in class, we will denote the set of rational numbers with Q. First, we will look at fundamental
properties of addition on Q .

Q is closed under addition. This means that when we add two rational numbers, the result is
also a rational number. Here is the justification. Let x and y be rational numbers. (The shorthand
notation for this is to say x, y ∈ Q. The symbol ∈ means “element of.”) This means that there
exist some integers m, n, p, q such that n, p ≠ 0 and x = m/n and y = p/q. We want to convince
ourselves that x + y is also a rational number. To be a rational, we must be able to write it as
a quotient of two integers (with the denominator not 0 of course). So let’s see if that is really
possible. We know that to add fractions, we first need to bring them to a common denominator .
We can use nq, as it is a common multiple of n and q. So

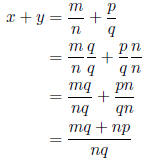
That certainly looks like a quotient , but is it a quotient of two integers? We know m and q are
integers, so their product must also be integer. Similarly, n and p are integers, so their product
must also be integer. Hence mq + np is the sum of two integers , and is therefore itself an integer.
That takes care of the numerator . The denominator is nq which is a product of two integers and
is therefore integer. That’s good. But could it be 0? A product is 0 when one of its factors is 0.
We know that n, q ≠ 0, and so their product cannot be 0. This shows x + y is a quotient of two
integers, and the one at the bottom is not 0. So x + y is indeed a rational number.

Addition of rational numbers is commutative. That is if x, y ∈ Q, then x + y = y + x.
Always. Here is why. Again, since x, y ∈ Q, we know that there exist some integers m, n, p, q such
that n, p ≠ 0 0 and x = m/n and y = p/q. Now

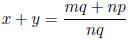
as we computed above. What about y + x?

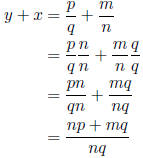
Since mq and np are integer numbers and we know addition is commutative on the integers,
mq + np = np + mq. Therefore

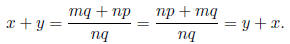
Addition of rational numbers is associative. This means that for any x, y, z ∈ Q, we have
(x+y)+z = x+(y +z). You probably don’t think very much of this, except possibly “Of course,
how could it be any other way?” Well it could be. There are algebraic systems and operations
which are not associative. They are hard to work with. Associativity is a very useful property even
if we take it for granted in lower mathematics . We can justify associativity in much the same way
as commutativity. If x, y, z ∈ Q, then there exist integers m, n, p, q, r, s such that n, q, s ≠ 0 and
x = m/n, y = p/q, and z = r/s. Now go ahead and compute (x + y) + z.

(x + y) + z =

Similarly, compute x + (y + z)

x + (y + z) =

Explain why the two results are the same.

The number 0 is an additive identity in Q. This means that if x ∈ Q, then x + 0 = x.
(Also 0 + x = x, but since addition is commutative, this is the same thing anyway.) This is easy
enough to see. Since x ∈ Q, there exist integers m, n such that n ≠ 0 and x = m/n. Now

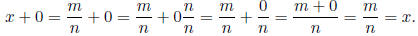
Now, you might think, what is the point of all this, I’ve known ever since 3rd grade that adding
0 to a number does nothing. Perhaps so, but what you probably knew was that your 3rd grade
teacher assured you this was so. Our goal is to understand the reasons why mathematics works
the way it does, and remembering what your 3rd grade teacher told you is good, but is not really
a reason why math is the way it is. In other words, the reason why 0 is an additive identity is not
because your 3rd grade teacher said so.

Every rational number has an additive inverse, which is also a rational number. This
means that if x ∈ Q then there exists a number y ∈ Q such that x + y = 0. (Also y + x = 0, but
this is the same thing because of commutativity.) Of course, we normally denote such a number y
by −x and we even know, form experience at least , that 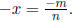So go ahead, convince me (and
yourself) that 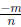is indeed additive inverse of x by adding it to x and showing that you get 0.
 

Now convince me that 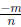is a rational number. (That is it satisfies the definition of a rational
number.)

Multiplication of rational numbers Multiplication has very much the same properties of
addition. I will list them and ask you to justify them. The justifications are similar to those we
gave about the properties of addition, only they are a little simpler .
Q is closed under multiplication.

Multiplication of rational numbers is commutative.

Multiplication of rational numbers is associative.

The number 1 is a multiplicative identity in Q.

Every nonzero rational number has a multiplicative inverse, which is also a rational
number.

Subtraction and division These don’t have so many nice properties. It is still true that Q is
closed under subtraction. You could justify this using a very similar argument to the one we had
for closure under addition. Try it:

Actually, a quicker way to do it is to note that x−y = x+(−y) and we already showed that the
additive inverse of a rational number is a rational number and the sum of two rationals is rational.
So as long as x, y ∈ Q, x − y must be rational.

Otherwise, subtraction is not commutative or associative, does not have an identity (no 0 does
not work because even though x − 0 = x, 0 − x ≠x), and therefore subtractive inverses cannot
exist either. Here is an easy challenge for you: show that subtraction is not commutative on Q by
finding two rational numbers x and y such that x − y ≠ y − x.

Looking at division, it doesn’t take long to notice that Q is not closed under division. The
problem is the number 0. If we remove it, the set of nonzero rational numbers (this is usually
denoted as Q* ) is closed under division. Justify this.

Finally, division is not commutative or associative, has no identity and therefore no inverses
either.