GRAPHING
Description
The student will learn how to avoid common pitfalls, how to shade from the “Y=”
menu, and options
to format the graphing screen .
Previously Learned Skills
1. Basic Graphing Calculator Usage Lessons
2. 2.1 Entering the Function
Lesson 2.2 Common Pitfalls – Plot Mode , Subtract vs Opposite, Fractional
Exponents
1. Turn on your calculator and clear the memory.
A Common Pitfall is to activate the Plot Menu instead of remaining in the Graph
Menu.
Key “Y=” the gray button below the screen on the left side. You will see:
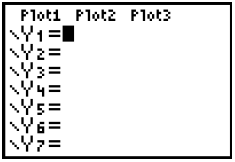
Notice where the cursor is located and that
the = sign is not in front of a black box.
2. Notice that the words at the top of the screen, “Plot1 Plot2 Plot3” are
NOT in front of a dark box.
This screen is correct. Sometimes students accidentally activate the “Plot1”
option, by keying
the blue gray “2nd” button (1, 1) followed by the “Y=” button, giving a new
screen seen below on the
left: Then in haste a student may key “ENTER” once or twice and activate the
PLOT Option of the
calculator which is used in a statistic class, not college algebra.
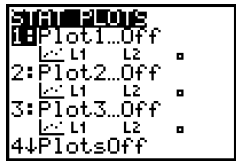
Entering the STAT PLOTS Menu
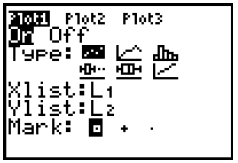
Choosing Plot 1 to be on
When we graph functions we do NOT plot points and create
broken line graphs , bar graphs,
Box and Whisker Plots as shown in the “Type:” of graphs used in Statistics
Classes.
3. The student then realizes that he is in an unusual menu
so keys “2nd” (1, 1) “MODE” (1, 2)
Which activates the “QUIT” option, returning the calculator to the HOME SCREEN
shown
at the left below. However, when the student now asks for the “Y=” menu, the
calculator is
ready to PLOT as seen with the “Plot1” now activated.
Notice the dark background behind the “Plot1,” show at the right below.

By keying “QUIT” we return to the Home Screen
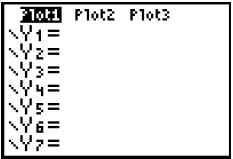
By keying
“Y=” we are now in the PLOT Mode
4. If the student then enters any function and keys “GRAPH” the calculator will
produce an
“ERR: INVALID DIM” and ask you to “1: Quit.” When you key “ENTER”, the
calculator
returns you to the Home Screen.
This error message is not very helpful so the student has to realize that he has
to deactivate the “Plot1.”

5. To deactivate the “Plot1” follow these steps:
(a) Key the blue gray button “2nd” (1, 1), once again seeing:
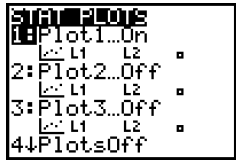
(b) Scroll down using the non-destructive gray arrow to “4:PlotsOff” and key “ENTER.”
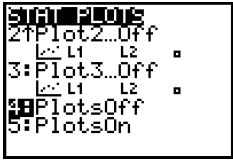
Scroll down to “4:PlotsOff”
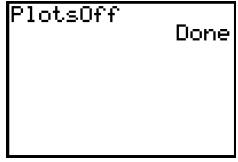
Key “ENTER” twice.
(c) You did it!!! Now you can resume graphing. Key “Y=” as
before and the “Plot1” is NOT
in front of a black rectangle and so not active.
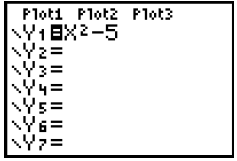
The calculator is in the GRAPH mode
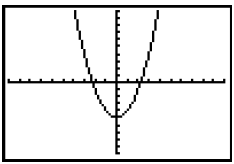
The graph of a
quadratic function is a parabola.
The quadratic function has degree 2, has 2 directions (down and up), and has 2
zeroes
(2 real solutions or 2 x- intercepts ).
NOTE:
You can also clear the DEFAULTS of your calculator to return to the
GRAPHING
Mode. However you may not want to clear, depending on your work.
6. Another Common Pitfall is to incorrectly using the subtraction sign " "found
on the gray
key on the right edge of the keypad or the opposite sign “( - )” (9, 4)
(a) At the beginning of the right side of the equation you must use the opposite
sign “ ( - )”
(b) Within a mathematical equation you must use the subtraction sign.
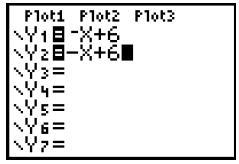
Y1 is correct while Y2 is incorrect
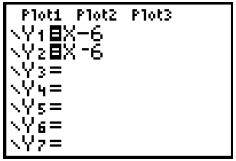
Y1 is correct while Y2 is incorrect
7. A third Common Pitfall is to enter fractional exponents
incorrectly.
If you want to take a square root of a number or a variable you have at least 2
easy
ways to accomplish this. There is a 3rd way using the “MATH” button which will
not be
discussed.
(a) You can use the square root symbol found on the left edge of your keypad by
keying “2nd” (1, 1) followed by “ x2 ” (4, 1) or
(b) Keying the “^” caret (4, 5) followed by the expression (1/2). Note that the
1/2 has
to be enclosed in parentheses ! If not, the calculator will take the number or
variable
to the first power and then divide by 2.
The principal square root of 9 is 3, not 4.5.
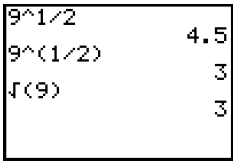
The first line is not correct. The 2nd and 3rd lines are
correct.
NOTE: Any radical power can be expressed as a fractional exponent. For example
the fifth root
of 32 squared is 4. 32 ^ (2/5) = 4
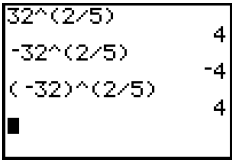
The first line tells the calculator to find the 5th root
of 32
which is 2 and then square that which is 4.
The 2nd line tells the calculator to find the 5th root of 32 which is 2, square
that which is 4 and
lastly take the opposite which is negative 4.
The 3rd line tells the calculator to find the 5th root of negative 32 which is
negative 2 and then
square the negative 2 which is positive 4.
In other words, the calculator does the root first, then the power.
Assignment 2.2 Common Pitfalls
Complete this assignment to submit to your instructor.
1. To enter an exponent on x, we use the “^” which is called the
___________________________
2. Explain how you know when you are in the “Plot1” Mode?
______________________________
3. Explain how you can turn off the “Plot1” Mode without clearly the DEFAULTS.
______________
____________________________________________________________________________
____________________________________________________________________________
4. When is the opposite sign used?
__________________________________________________
5. When is the subtraction sign used?
________________________________________________
6. How can you tell which sign is which, the subtraction sign and the opposite
sign? ____________
_____________________________________________________________________________
Explain how the calculator finds the following:
7. The fourth root of 16 cubed. 16 ^ (3/4) = 8
____________________________________________
______________________________________________________________________________
8. The cube root of negative 125 squared. (-125) ^ (2/3) = 25
_______________________________
_____________________________________________________________________________
9. The 5th root of negative 243 squared. (-243) ^ (2/5)
____________________________________
______________________________________________________________________________
10. The opposite of the 5th root of negative 243 squared. – ( - 243) ^ (2/5)
______________________
______________________________________________________________________________
| Prev | Next |