Functions and Models
This chapter is mostly a review of pre-calculus., in
conjunction with part of the preview assignments .
In class we cover just the last two sections , on exponentials and logarithms ,
plus topics that
come up from questions on the preview assignment.
The exercises for this chapter start with four online
WebAssign diagnostic assignments. These
correspond to the diagnostic tests near the front of the textbook, but submit
your answers online
even if you work them all out on paper first; partly to learn how to use
WebAssign before we start
on the graded assignments.
A function like f (x) = 2x is called exponential because
the argument x is the exponent in the
formula. Exponential functions are the most basic and common transcendental
functions, and are
probably the most important functions in mathematics and science after
polynomials . So this is
the early encounter mentioned in the sub-title of the text.
We will see how exponential functions can be defined to
have graphs that are continuous , unbroken
curves with well defined slopes, rather being only a collection of separate
points for integer values
of x.
Non-negative integer powers of 2
With basic algebra, exponential functions are defined first for positive
integer arguments, by formula
2n = 2· 2 · 2 · · · 2, the product of n factors 2.
Then to satisfy the rule
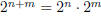for the case m = 0 requires
20 = 1
so all non-negative integers n are covered.
Negative integer powers of 2
For a negative integer n, |n| = −n is positive, and to satisfy the rule
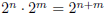we must have
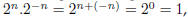and so dividing by
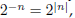
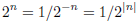for n a negative integer.
Rational powers of 2
Next we can make sense of exponentials for rational exponents. To get the
exponential 2r for any
rational number r start with exponent 1/q, q a positive integer. To satisfy the
rule
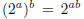
requires
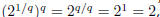so
taking the q-th root of both sides of this equation,
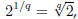the q-th root of 2, for q a positive integer.
Finally, any rational number can be written as r = p/q
with p an integer, q a positive integer, and
the same rule requires
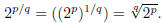
Irrational powers of 2 (so all power of 2)
The graph of 2x for all rational x looks like a dense collection of dots
along a curve which increases
to the right. Can we fill in the gaps at irrational values of x and get an
smooth, uninterrupted
curve? For example, can we make sense of an irrational power like
?
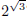A number like
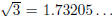is approximated by a succession of decimal fractions 1, 1.7, 1.73,
1.732, 1.7320, 1.73205 and so on: it is the limit of this sequence of rational
numbers. Raising 2 to each
of these powers gives the following new sequence of numbers (everything rounded
to five decimal
places):
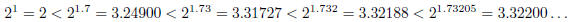
All of these should be less that
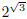since the values are increasing as the exponent increases and
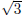is greater than each of these exponents. On the other hand if we round up the
decimal approximations
of
,
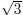the exponentials should all be greater than
:
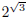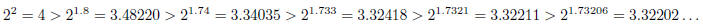
So it appears that
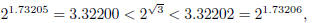
so that
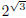rounded to four decimal places is 3.3220.
We could continue with either sequence to compute a value
for
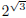to as many decimal places as
we wish. In this way, we can make sense of, and compute, any power of 2,
rational or irrational,
so we have made sense of the exponential function f(x) = 2x for all real
arguments x.
Irrational powers of any positive number
There is nothing special about the base 2 used above except that it is
positive: we could do the same
thing with any positive real number a, to compute the exponential function f(x)
= ax. The graphs
for the different functions vary mostly in that they are increasing for a > 1,
and increase faster for
larger values of a, and are decreasing for 0 < a < 1, decreasing faster for
smaller values of a. In the
borderline case of a = 1, the graph is a constant: 1x = 1.
Rules for Exponential Functions
The familiar rules for exponentials still hold just as with with rational
exponents: for a and b
positive and any real numbers x and y,
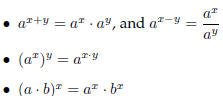
Applications of Exponential Functions
The textbook does an example of population growth which we will see again
later. For variety, let
us look at radioactive decay.
ADDED EXAMPLE A The half-life of strontium-90,
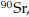is 25 years. This means that half of any
given quantity of
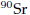will disintegrate in 25 years.
a. If a sample of
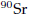initially has a mass of 24mg, find an expression for the mass m(t) that
remains after t years.
b. Find the mass remaining after 40 years, correct to the nearest milligram.
c. Use a graphing device to graph m(t) and use the graph
to estimate the time required for the
mass to be reduced to 5 mg .
The number e
Of all possible choice of the base a of an exponential function ax, one is
most convenient for mathematics
because it makes the slope of the graph simplest : the number called e whose
value is
approximately e ≈ 2.71828.
The graphs of all exponential functions pass through the
point P(0, 1) on the y-axis, but the bigger
a is, the faster the function value grows as x increases, so the greater the
slope is at this point. The
slope is zero for a = 1, when the function is constant, and increases as a
increases. Experimenting
with a graphing calculator suggests that the slope is less than 1 for 2x, but
greater than 1 for 3x.
So it seems that by increasing a to somewhere between 2 and 3, the slope will be
1 at P(0, 1), with
the slope greater than 1 for greater values of a, less than 1 for lesser values.
That is, there is just one
special value for the base that gives slope 1: this is the value called e. We
have already seen that
e lies between 2 and 3, and with ever more careful computation of slopes we
could calculate the
more accurate value given above.
We will soon see that any other exponential function can
be written in terms of ex, and this is very
convenient in calculus, making this particular exponential function so important
that it is often
called simply “the exponential function”.
Homework Exercises 1, 2, 7, 8, 17, 18, 25.
| Prev | Next |