Composition of Functions

Composition of the function f with the function g, given by 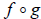, is defined by:

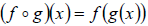
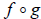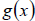Domain of consists of all x in domain of g such that is in the domain of f.

Example. :If 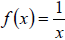and 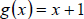, find:

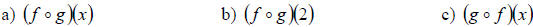
Example: Use the graphs of f and g to evaluate each expression.

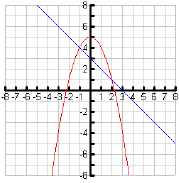
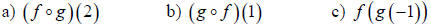
Example: In the example above, for what value (s) of x is ?

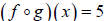Horizontal Compression and Elongation of Graphs . If ,
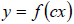a) For any constant 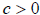, the graph of 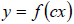is the same as that of 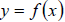with a
change in the horizontal scale.

1) If 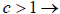horizontal compression

2) If 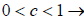horizontal elongation
b) The grap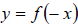h of is a reflection about the y-axis of the graph of .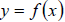

1) For 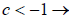horizontal compression and reflection.

2) For 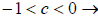horizontal elongation and reflection.

Example: Graph the following functions:

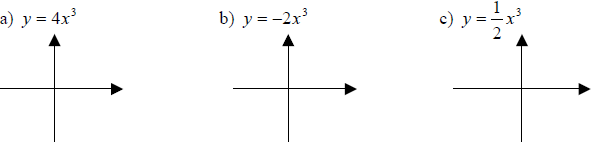
Example: If , 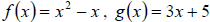, and 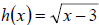, find:

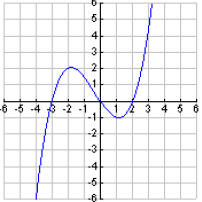
Example: Use the graph of the function given below to sketch the graph of the indicated
functions.

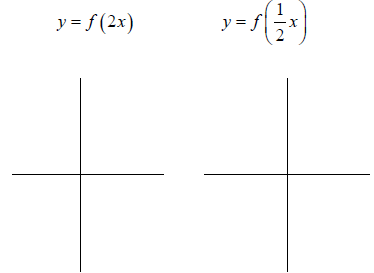
Example: Write the function 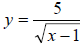as the composition of three functions.


Applied Example: The number of bacteria in a refrigerated food is given by
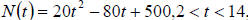where t is the Celsius temperature of the food. when
the food is removed from refrigeration , the temperature is given by
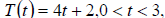where t is the time in hours.

a) What does the composite function 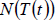represent?

b) How many bacteria are in the food when t=2 hours?