Co-Calculus Homework 2 Solutions
Find all real zeros of the following polynomials. Write
each polynomial in factored
form.
6. f(x) = x3 − 6x2 + 11x − 6
Solution :
First of all, since f is a polynomial of degree 3, we know that f has at most 3
real zeros . Second, the coefficients in front of the powers of x in f(x) change
sign 3
times (1 → −6 → 11 → −6), so f(x) has either 3 positive real zeros or 3-2=1
positive
real zero. Note that
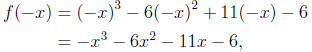
so we see that the coefficients of f (−x) have NO sign changes, so f(x) has no
negative
real real zeros.
To find the potential rational zeros of f, we use the Rational zeros theorem,
which
says that, if x is a zero of f, then it must be of the form
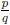 , where p is a factor of the
, where p is a factor of the
coefficient in front of x0 = 1, and q is a factor of the coefficient
in front of xn, where
n is the highest power of x in the polynomial . In this case, possibilities for p
include
1,-1,2,-2,3,-3, 6, or -6, and possibilities for q include 1 and -1. So possible
RATIONAL
zeros of f include 1,-1,2,-2,3,-3, 6, or -6. Let’s test x = 1. Plugging x = 1
into f(x)
gives f(1) = 1 − 6 + 11 − 6 = 0. Great news! This means 1 is a zero of f, so x −
1 is
a factor of f. So f(x) = (x − 1)q(x), where q(x) is a polynomial. To solve for
q (x),
we use long division:
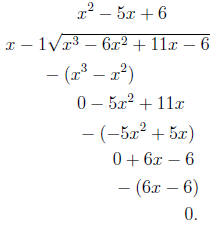
This means f(x) = (x − 1)(x2 − 5x + 6). To find
other zeros of f, we can just
find the other factors of f, and to do this, we simply factor (x2 −
5x + 6). We get
(x2 − 5x + 6) = (x − 2)(x − 3) (you can use the quadratic formula to
do this) . So,
finally,
f(x) = (x − 1)(x − 2)(x − 3),
and the zeros of f are given by 1, 2, and 3. Again this follows because (x−1),
(x−2),
and (x − 3) are factors of f!
9. f(x) = x4 − 10x3 + 35x2
− 50x + 24
Solution:
First of all, since f is a polynomial of degree 4, it has at most 4 real zeros.
Since
the coefficients of f(x) change sign 4 times, f has either 4, 4-2=2, or 4-4=0
positive
real zeros; that is, f has either 4,2, or 0 positive real zeros (recall it is
the number
of sign changes or the number of sign changes minus an even integer). To
determine
the possible number of negative real zeros, we write
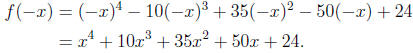
Since coefficients of f(−x) never change sign, we conclude that f has NO
negative
real zeros.
Using the Rational zeros theorem, we list the potential rational zeros of f.
Using
the same strategy as in problem 5 above, we get that potential rational zeros
are:
1, -1, 2, -1, 3, -3, 4, -4, 6, -6, 8, -8, 12, -12, 24, -24. We can eliminate all
negative
numbers from the list since f has no negative real zeros, so possible rational
zeros of f include 1, 2, 3, 4, 6, 8, 12, and 24. We test x = 1, and we find that
f(1) = 0. So (x − 1) is a factor of f, which means f(x) = (x − 1)q(x), where
q(x)
is a polynomial. To determine q(x), we use long division (which I leave to you),
and we get f(x) = (x − 1)(x3 − 9x2 + 26x − 24).
Unfortunately, we cannot factor
q(x) = x3 − 9x2 + 26x − 24 in our heads (at least I
can’t), so we need to factor q(x)
by determining its zeros. Note that the rational zeros for q must come from the
list
of potential rational zeros for our original polynomial f, because if x−c is a
factor of
q(x), then it is also a factor of f(x) (meaning if c is a zero of q, then it is
also a zero
of f). So we go back to our list and test x = 1 AGAIN to see if x = 1 is a zero
of q(x)
(its possible that x−1 is a factor that shows up twice in f(x)). In this case
q(1) ≠ 0.
Luckily, q(2) = 0, so x−2 is a factor of q(x). Now, q(x) = (x−2)r(x), where r(x)
is a
polynomial. To determine r(x), we use long division, and we get r(x) = x2
−7x+12,
and q(x) = (x−2)(x2−7x+12), so f(x) = (x−1)q(x) = (x−1)(x−2)(x2−7x+12).
To finish finding zeros of f and factoring f, we just need to factor x2
− 7x + 12 =
(x − 4)(x − 3). So
(1) f(x) = (x − 1)(x − 2)(x − 4)(x − 3)
f(x) = (x − 1)(x − 2)(x − 4)(x − 3)
and the zeros of f are 1, 2, 3, and 4.
11. f(x) = 9x6 + 44x4 + 31x2 − 4
Solution:
First of all, f is a polynomial of degree 6, so it has at most 6 real zeros.
Using
Descartes rule of signs, we see only one sign change in coefficients of f(x), so
f has
exactly one positive real zero. Note that
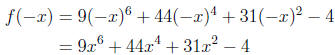
which, again, has only one sign change, so f has exactly one NEGATIVE real zero.
This is very useful information, because now we know that f has exactly two real
zeros: one positive and one negative. Once we find them, we will know that we
can
stop working. Also, since f(x) = f(−x), we can conclude that if x = c is a zero
of
f(x), then x = −c is a zero of f(x), so we really only need to find one zero of
f.
Using the rational zeros theorem, we see that potential rational zeros include
1, -1, 2,
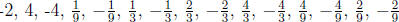 . Certainly, 1, -1, 2, -2, 4, and -4
. Certainly, 1, -1, 2, -2, 4, and -4
will not work, because when you plug them in, you will get a large number minus
4.
After some testing, we find that 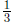 works, and
by the logic above ,
works, and
by the logic above , 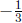 works as well.
works as well.
We have found all of the real zeros. We know by the factor theorem that
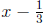 and
and
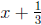 are factors of f, that is,
are factors of f, that is,
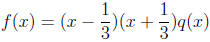
where q(x) cannot be factored (since f has no other real zeros). To find q(x),
we use
long division to divide 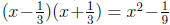 into f(x). We get
q(x) = 9x4+45x2+36.
into f(x). We get
q(x) = 9x4+45x2+36.
So, finally,
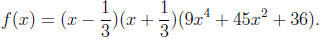
We cannot factor f any further. The real zeros of f are
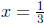 and
and 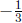 .
.
| Prev | Next |