Classification of Differential Equations
Once we have written a differential equation in the form
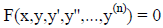
We can talk about whether a differential equation is
linear or not .
We say that the differential equation above is a linear differential equation if
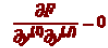
for all i and j. Any linear ordinary differential equation of degree n can be written as
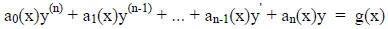
Examples
3x2y'' + 2ln(x)y' + ex y = 3xcos x
is a second order linear ordinary differential equation.
4yy''' - x3y' + cos y = e2x
is not a linear differential equation because of the 4yy''' and the cos y terms .
MyPhysicsLab – Classifying Differential Equations
When you study differential equations, it is kind of like botany. You learn to
look at an
equation and classify it into a certain group . The reason is that the techniques
for solving
differential equations are common to these various classification groups. And
sometimes
you can transform an equation of one type into an equivalent equation of another
type, so
that you can use easier solution techniques . Here then are some of the major
classifications of differential equations:
First Order, Second Order, etc.
The order of a differential equation is equal to the highest derivative in the
equation. The
single-quote indicates differention. So x' is a first derivative, while x'' is a
second
derivative. x' = 1/x is first-order x'' = −x is second-order x'' + 2 x' + x = 0
is second-order.
Linear vs. Non-linear
Linear just means that the variable in an equation appears only with a power of
one . So x
is linear but x2 is non-linear. Also any function like cos(x) is non-linear.
In math and physics , linear generally means "simple" and non-linear means
"complicated". The theory for solving linear equations is very well developed
because
linear equations are simple enough to be solveable. Non-linear equations can
usually not
be solved exactly and are the subject of much on-going research. Here is a brief
description of how to recognize a linear equation.
Recall that the equation for a line is y = m x + b where m, b are constants ( m
is the slope ,
and b is the y- intercept ). In a differential equation, when the variables and
their
derivatives are only multiplied by constants , then the equation is linear. The
variables
and their derivatives must always appear as a simple first power. Here are some
examples.
x'' + x = 0 is linear x'' + 2x' + x = 0 is linear x' + 1/x = 0 is non-linear
because 1/x is not a
first power x' + x2 = 0 is non-linear because x2 is not a first power x'' + sin(x) = 0 is nonlinear
because sin(x) is not a first power x x' = 1 is non-linear because x' is not
multiplied by a
constant Similar rules apply to multiple variable problems. x' + y' = 0 is
linear x y' = 1 is
non-linear because y' is not multiplied by a constant Note, however, that an
exception is made
for the time variable t (ie. the variable that we are differentiating by). We
can have any
function of t appear in the equation, but still have an equation that is linear
in x. x'' + 2 x'
+ x = sin(t) is linear in x x' + t2x = 0 is linear in x
Linear vs. non-linear
Linear differential equations do not contain any higher powers of any
differentials, nonlinear
differential equations do. In fully linear differential equations, higher powers
of the
independent variable(s) are also excluded.
Examples:
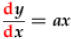and
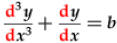are ODE, but
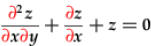and
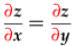are
PDE.
All of the examples above are linear, but
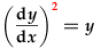isn't. Note that
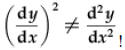
| Prev | Next |