Algebra 2B
Credit By Exam Review Sheet
This Credit By Exam Review Sheet can help you prepare for the exam by giving you
an idea of
what you need to study, review, and learn. To succeed, you should be thoroughly
familiar with
the subject matter before you attempt to take the exam.
Every question that appears on the Credit by Exam/Examination for
Acceleration is grounded in
the knowledge and skills statements and student expectations within the
state-mandated
standards, the Texas Essential Knowledge and Skills (TEKS). It should be noted
that an exam
will not test every student expectation. However, it is important that students
study and know
the entire scope of the TEKS so that they can develop a complete understanding
of the content.
The CBE/EAs are a global exam grounded in the TEKS and are not designed to be a
final exam
for the University of Texas high school courses. Since questions are not taken
from any one source, you can
prepare by reviewing any of the state-adopted textbooks.
About the exam
The Credit By Exam consists of 40 multiple-choice questions that are worth 1
point each. You
will be allowed 3 hours to take the exam and you will be allowed to use a
graphing calculator .
Concepts and Objectives
The bulleted list and sample questions below may not refer to all the material
that will be in the
exam. This list only provides additional information for some of the student
expectations tested
in the Algebra 2 Second Semester Credit by Exam. The use of problem-solving
skills is
important; all problem-solving activities require more than one step. In
addition, you may be
asked to use algebra and arithmetic skills from previous math courses . To
prepare for this exam
refer to the Texas Essential Knowledge and Skill for Algebra 1, Geometry, and
Algebra 2.
Ultimately, you should use the TEKS to guide your exam preparation
In Algebra 2B, you learned about rational functions, exponential and
logarithmic functions , and
conic sections. On the exam, you should be able to:
• use the area formula for rectangles to write quadratic function rules and to
solve problem
situations
• determine a possible quadratic equation given the zeros
• determine the characteristics of the discriminant given a quadratic function
rule or graph
• determine if a quadratic equation has one , two, or no solutions
• identify a rational function given words that describe a problem situation, a
table, a graph, or
a function rule
• use words to a describe a rational function given a table, a graph, or a
function rule
• make a table of values for a rational function rule given words that describe
a problem
situation, a graph, or a function rule
• graph a rational function rule given words that describe a problem situation,
a table, or a
function rule
• write a rational function rule given words that describe a problem situation,
a table, or a
graph
• interpret the meaning of specific points that make a rational function true
• describe the domain and range of a rational function
• identify the dependent and independent variables of a rational function
• find the x- intercepts and y -intercepts for a given rational function
• find the vertical and horizontal asymptotes for a rational function
• describe how changing a rational function rule shifts the graph to the left or
right and up or
down from the parent function
• solve rational equations and inequalities by using graphical and symbolic
methods
• write an exponential function rule and solve for specific values given a
problem situation (for
example, solve problems involving carbon-14 dating, population, compounded
interest, and
continuous compounded interest)
• interpret the meaning of specific points that make an exponential function
rule true
• graph exponential functions
• describe how changing an exponential function rule shifts the graph to the
left or right and up
or down from the parent function
• simplify exponential expressions, including problems with fractions as
exponents
• solve exponential equations graphically and symbolically , including problems
with fractions
as exponents
• find the inverse of an exponential or logarithmic function
• provide a table of values that represents the inverse of a logarithmic or
exponential function
• graph the inverse of a logarithmic or exponential function
• rewrite exponential equations in logarithmic form
• rewrite logarithmic equations in exponential form
• find the value of logarithmic expressions
• estimate the value of logarithmic expressions
• use properties of logarithms to solve exponential and logarithmic equations
• describe the behavior of the graph of a logarithmic function with restrictions
placed on the
value of the base of the logarithm
• describe how changing a logarithmic function rule shifts the graph to the left
or right and up
or down from the parent function
• state the domain and range, the asymptotes, the x-intercepts and y-intercepts,
and graph
logarithmic functions
• use properties of logarithms to write expressions in a condensed form
• use properties of logarithms to solve problem situations (for example,
population growth
problems)
• identify conic section equations for circles, parabolas, ellipses, and
hyperbolas
• find the axis of symmetry, vertex, directrix, and focus for a parabola
• write an equation for a parabola given the focus and directrix
• find the center, foci, and vertices on the major axis for an ellipse
• write an equation for a ellipse given the vertex, center and focus
• find the center and radius of a circle
• write an equation for a circle given the center and radius
• find the center, foci, vertices, and asymptotes for a hyperbola
• write an equation for a hyperbola given the vertex and focus
• graph circles, parabolas, ellipses, and hyperbolas
• write equations in standard form for circles, parabolas, ellipses, and
hyperbolas
• solve problem situations that are described as a parabola
• identify quadratic or square root functions given words that describe a
problem situation, a
table, a graph, or a function rule
• use words to describe quadratic or square root functions given a table, a
graph, or a function
rule
• make a table of values for quadratic or square root functions given words that
describe a
problem situation, a graph, or a function rule
• graph quadratic or square root functions given words that describe a problem
situation, a
table, or a function rule
• write quadratic or square root function rules given words that describe a
problem situation, a
table, or a graph
• describe the domain and range of quadratic and square root functions
• describe how changing a quadratic or square root function rule shifts the
graph to the left or
the right, shifts the graph up or down, and dilates or compresses the graph
• solve quadratic and square root equations and inequalities by using graphical
and symbolic
methods
• find and graph the inverse function for a quadratic function or a square root
function
• solve quadratic equations by factoring , graphing, using a table, completing
the square, and
the quadratic formula
Sample Questions
These sample questions will give you a better idea of the types of questions you
can expect on
the Credit By Exam. These questions are provided to illustrate the format of the
exam; they are
not a duplicate of the actual exam. In order to be successful on the exam, you
must study and
review all of the concepts listed above.
Multiple-Choice
This part contains 5 multiple-choice questions. Circle the letter of the correct
response to each of
the following questions.
1. What is the value of log24?
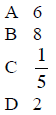
2. What does the following equation represent?
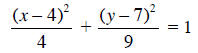
A Circle
B Parabola
C Ellipse
D Hyperbola
3. Which rule best matches the data in the table below?
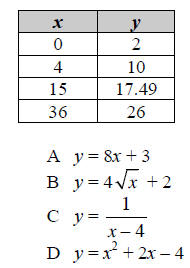
4. Which graph represents the equation
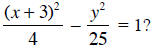
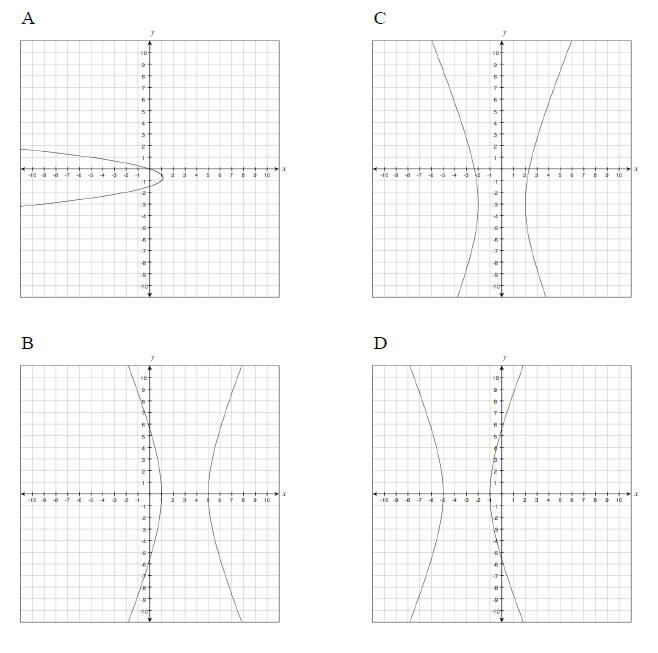
5. Ricardo has a rectangular garden. The width of the
garden is two feet shorter than the
length. Which equation represents the area of the garden?

Answer Key
| Item Number | Correct Answer | TEKS |
| 1 | D | (b)(2A.11)(D) |
| 2 | C | (b)(2A.5)(D) |
| 3 | B | (b)(2A.9)(B) |
| 4 | D | (b)(2A.5)(B) |
| 5 | D | (b)(2A.8)(A) |
| Prev | Next |