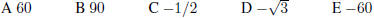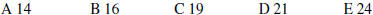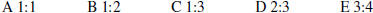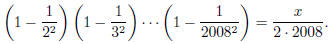2008 LSU Math Contest
|
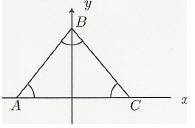
14 Suppose the equation x 2+bx+4 = 0 has exactly one solution. The best statement about b is: A b must be equal to 4 B b must be equal to −4 C b must be equal to 2 D b must be equal to −2 E none of the above |
|||
|
15 Of the following statements, the one that is incorrect is: A Doubling the base of a rectangle doubles the area. B Doubling the altitude of a triangle doubles the area. C Doubling the radius of a circle doubles the area. D Doubling the denominator of a positive fraction and dividing its numerator by 2 changes the fraction . E Doubling a given number may make it less than it originally was. |
|||
|
|||
|
17 During the final game of a basketball tournament, only 7 players from the tournament winning team played. The scoring average of all 7 players was 13. The scoring average of everyone but the point guard was 12. How many points did the point guard score?
|
|||
|
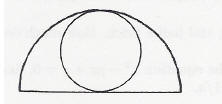
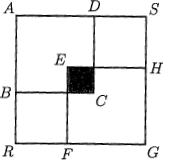
18 A small circle just fits inside a semicircle. What is the ratio of the area of the small circle to the area of the semicircle containing it?
|
|||
|
Questions 19 - 28 Exact Answers These next ten questions require exact numerical or algebraic answers. Hand-written exact answers must be written on the answer sheet with fractions reduced , radicals simplified, and denominators rationalized (Improper fractions can be left alone or changed to mixed fractions). Do not make an approximation for π or other irrational numbers. Answers must be exact. Large numbers should not be multiplied out , i.e., do not try to multiply out 20! or 640. |
|||
|
19 An airport has a moving sidewalk. Standing on the moving sidewalk, Joe takes 3 minutes to reach the end. Walking next to the moving sidewalk, Joe takes 4 minutes to reach the end. How long does it take Joe to reach the end if he walks on the moving sidewalk? |
|||
|
20 John earned some money. When he was paid, his employer had already deducted 20% federal and 2% state income taxes. He was paid $792. How much, to the nearest dollar, did he earn? |
|||
|
21 A six place number is formed by repeating a three place number: For example, 256,256, or 678,678, etc. Call these numbers copycats. Find greatest common divisor of all the copycats. |
|||
|
|||
23 For how many different positive integers
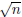 does differ does differfrom 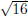 by less than 1? by less than 1? |
|||
| 24 What is the last digit of 22008? | |||
|
25 Let
Compute the integer x. |
|||
|
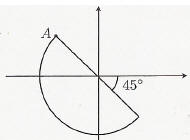
26 A line is called a supporting line of a figure if the line meets the figure but the whole figure is on one side of the line. For example, the line that contains the side of a square is a supporting line of the square. Consider the figure below drawn on the coordinate plane - it is half of the unit circle.
If a supporting line passes through A, then how
large of |
|||
|
27 Suppose A and B are points on the circle with center C. The angle ∠ACB is 30°. If a point D is randomly chosen on the circle, then what is the probability that the triangle ΔABD is obtuse? |
|||
|
28 A room is 30 feet square and 12 feet high. A spider is located in one of the corners on the floor. An unsuspecting fly rests at the diagonally opposite corner on the ceiling. If the fly does not move, what is the shortest distance the spider must crawl, always touching a surface of the room, to catch the fly? |
|||
|
Tie Breaker Please give a detailed explanation on the answer sheet to your solution to Question 28 above. This tie breaker question is graded as an essay question i.e., it is graded for the clarity of explanation and argument as well as correctness. It is the only question graded for partial credit. It is graded only to separate first, second, and third place ties. |
| Prev | Next |