Solving Quadratic Equations
22.3 Solution by Completing the Square
We have seen that expressions of the form :
a2x2 − b2
are known as differences of squares and can be factorised as follows:
(ax − b)(ax + b).
This simple factorisation leads to another technique to solve quadratic
equations known as
completing the square.
We demonstrate with a simple example, by trying to solve for x in :
x2 − 2x − 1 = 0. (22.1)
(22.1)
We cannot easily find factors of this term , but the first two terms look similar
to the first two
terms of the perfect square:
(x − 1)2 = x2 − 2x + 1.
However, we can cheat and create a perfect square by adding 2 to both sides of
the equation in
(22.1) as:
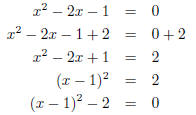
Now we know that:
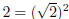
which means that:
(x − 1)2 − 2
is a difference of squares. Therefore we can write:
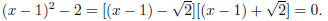
he solution to x2 − 2x − 1 = 0 is then:
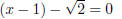
or
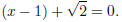
This means 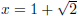 or
or
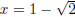 . This example demonstrates the use of
completing the
. This example demonstrates the use of
completing the
square to solve a quadratic equation .
Method : Solving Quadratic Equations by Completing the
Square
1. Write the equation in the form ax2 + bx + c = 0. e.g. x2
+ 2x . 3 = 0
2. Take the constant over to the right hand side of the equation. e.g. x2
+ 2x = 3
3. If necessary, make the coefficient of the x 2 term = 1, by dividing
through by the existing
coefficient.
4. Take half the coefficient of the x term, square it and add it to both sides
of the equation.
e.g. in x2 + 2x = 3, half of the x term is 1. 11 = 1.
Therefore we add 1 to both sides to
get: x2 + 2x + 1 = 3 + 1.
5. Write the left hand side as a perfect square: (x + 1)2 - 4 = 0
6. You should then be able to factorise the equation in terms of difference of
squares and
then solve for x: (x + 1 - 2)(x + 1 + 2) = 0
 |
Worked Example 106: Solving
Quadratic Equations by Completing the Square Question: Solve: x2 − 10x − 11 = 0 by completing the square Answer Step 1 : Write the equation in the form ax2 + bx + c = 0 x2 − 10x − 11 = 0 Step 2 : Take the constant over to the right hand side of the equation x2 − 10x = 11 Step 3 : Check that the coefficient of the x2 term is 1. The coefficient of the x2 term is 1. Step 4 : Take half the coefficient of the x term, square it and add it to both sides The coefficient of the x term is 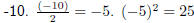 .
Therefore: .
Therefore:x2 − 10x + 25 = 11 + 25 Step 5 : Write the left hand side as a perfect square (x − 5)2 − 36 = 0 Step 6 : Factorise equation as difference of squares (x − 5)2 − 36 = 0 [(x − 5) + 6][(x − 5) − 6] = 0 Step 7 : Solve for the unknown value [x + 1][x − 11] = 0 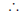 x = −1 or x = 11 x = −1 or x = 11 |
 |
Worked Example 107: Solving
Quadratic Equations by Completing the Square Question: Solve: 2x2 − 8x − 16 = 0 by completing the square Answer Step 1 : Write the equation in the form ax2 + bx + c = 0 2x2 − 8x − 16 = 0 Step 2 : Take the constant over to the right hand side of the equation 2x2 − 8x = 16 Step 3 : Check that the coefficient of the x2 term is 1. The coefficient of the x2 term is 2. Therefore, divide both sides by 2: x2 − 4x = 8 Step 4 : Take half the coefficient of the x term, square it and add it to both sides The coefficient of the x term is 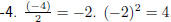 .
Therefore: .
Therefore:x2 − 4x + 4 = 8 + 4 Step 5 : Write the left hand side as a perfect square (x − 2)2 − 12 = 0 Step 6 : Factorise equation as difference of squares 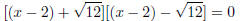 Step 7 : Solve for the unknown value 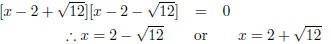 Step 8 : The last three steps can also be done in a different the way Leave left hand side written as a perfect square (x − 2)2= 12 Step 9 : Take the square root on both sides of the equation 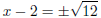 Step 10 : Solve for x Therefore 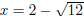 or or
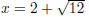 Compare to answer in step 7. |
|
Exercise: Solution by Completing the Square Solve the following equations by completing the square: |
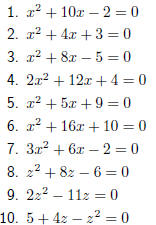
| Prev | Next |