Solving Quadratic Equations
A quadratic equation is of the form ax2 + bx + c = 0.
Solving an equation of this kind is
considerably more tricky than solving a linear equation . Fortunately, the
following method leads to
an easy formula that one could refer to when needed. Multiplying each term of
the equation by 4a,
4a2x2 + 4abx + 4ac = 0. Adding and subtracting b2, we get 4a2x2 + 4abx +
b2 - b2 + 4ac = 0.
Transferring the last two terms of the LHS to the RHS, 4a2x2 + 4abx + b2 =
b2 - 4ac. Note that
the LHS is now a perfect square of 2ax + b. Therefore, (2ax + b)2 = b2 - 4ac
which implies 2ax +
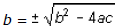. This process has transformed the original quadratic equation into a linear
one!
Since we know how to solve linear equations from the previous section, we can
write the solution
to the current problem as
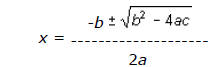
Example
Let us solve the equation x2 = -10 * x - 9. It may be rewritten as x2 +
10x + 9 = 0. Noting that a
= 1, b = 10 and c = 9 for the given equation , we have
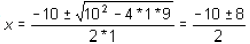Thus
there are 2 solutions to this equation : -1 and -9.
Application
Ming is considering a three-year investment in a development project. The
project will yield
positive returns of $1000 the first year for Ming, and negative returns of $100
and $1100 the
following two years. What bank rate of interest will make Ming indifferent
between investing in the
project and not investing in it?
To solve this problem, we need to figure out that rate of
interest which makes the present value of
the project equal to zero . (In economics, this special interest rate is called
the internal rate of
return of a project.) Thus 1000 - 100/(1 + r) - 1100/(1 + r)2 = 0. Multiplying
each term by (1 + r)
2, we get 1000 * (1 + r)2 - 100 * (1 + r) - 1100 = 0. Collecting powers of r,
10 * r2 + 19 * r - 2 = 0. Using the formula for solving a quadratic equation,
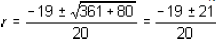which implies r is either -2 or 0.1. Neglecting the negative root , the
bank interest rate that makes Ming indifferent between investing in the project
or not is 10%.
| Prev | Next |