Solving for x
This lesson contains three parts that will present
practice problems
and videos to show you how to solve for x .
Part I
looks at solving first degree equations, and
indicates that in solving any equation, three
outcomes are possible:
• There is a unique solution(s)
• There is NO solution. This will happen if you
write an illogical equation.
• There are an infinite number of solutions .
When this happens, the equation is called an
identity.
Part II looks at solving second degree equations
Part III looks at using Excel’s Solver to solve
various
equations (future lesson)
Definition of Degree
The degree of an equation is equal to the largest exponent
of the variables in
the equation. It indicates the maximum number of solutions an equation can
have, and it assumes that all exponents are positive integers . For example,
x + 3 is a first degree equation. It can have at most
one solution.
x2 - 8x = 12 is a 2nd degree equation. It can have at
most
two solutions.
Part I: Steps to Solve a First Degree Equation ->
Part I: Steps to Solve for X, Working with a First Degree Equation
Step 1 If fractions are present, determine the Least
Common
Denominator . Multiply both sides by the LCD .
Step 2 Simplify both sides.
Step 3 Move all terms with x to the left side; move
everything
else to the right side. We can move terms from side to
side by changing the sign of the term .
Step 4 Simplify both sides.
Step 5 Divide both sides by the coefficient of x.
Practice Problem #1A: Solving First Degree Equations
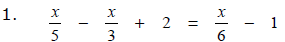
2. 5x + 7 - 2(3 - x) = 2x + 4 - 12
Answers to Practice Problem #1A: Solving First Degree Equations
1. x = 10
2.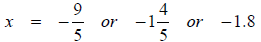
3. x = no solution
Part II: Steps to Solve a Second Degree Equation (x2 - 3x = 10)
These steps and the Quadratic Formula below will be
discussed in the
video that follows.
Step 1 If fractions are present, determine the
Least Common
Denominator. Multiply both sides by the LCD.
Step 2 Move everything to the left side. The right side must be 0.
Step 3 Simplify the left side, and if possible,
rewrite it in
completely factored form . If it does not factor, use the
Quadratic formula .
Step 4 Using the logic, that when the product of
two numbers
equals 0, then one of the numbers must be 0. Rewrite the
problem to create two first degree equations.
Step 5 Solve the two first degree equations.
Quadratic Formula
To solve ax2 + bx + c = 0
we use the Quadratic Formula
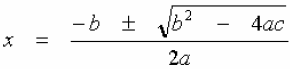
In the video, we solve this problem:
Given that: x = Number of calculators to produce
P(x) = Profit made on calculators produced
P(x) = -.42 + 40x - 640
How many calculators must be produced to break even?
Practice Problem #2A: Solving Second Degree Equations
1. x2 - 6x = 16
2. 2x2 - 14x - 36 = 0
3. x2 + 6x - 5 = 0
Use a calculator.
Answers to Practice Problem #2A: Solving Second Degree Equations
1. x = 8 or x = -2
2. x = 9 or x = -2
3.
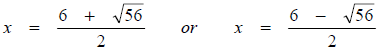
Using a calculator,
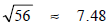
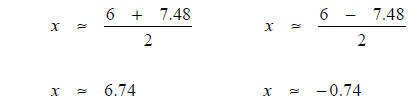
Part III: Future Lesson on Using Excel’s Solver
| Prev | Next |