Second derivative test

Last time: Max/Min problems. Least squares approximation.
Today: Second derivative test. Global max/min: Boundaries and infinity. Level curves and level surfaces.

Reading Material: From Simmos 19.1, 19.7. From the Lecture Notes SD.

2 Second derivatives

Given a function z = f(x, y) we denoted the first partial derivatives of f as

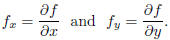
Then it is simple to define the second partial derivatives:

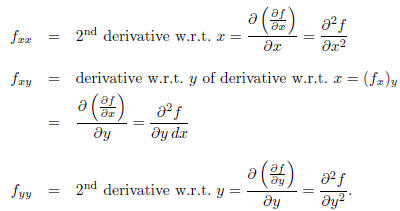
Remark. There is a very surprising theorem: if all second derivatives are continuous then

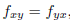
and this in fact is going to be the case for all functions we will be dealing with in this class->

3 2^nd derivative test

Last time we learned that for a function z = f(x, y) local max/min occur on critical pints, that is
on points (x₀, y₀) such that

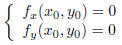
We also learned that not all critical points are either a local max or min, take for example the point
(0, 0) critical point for the function z = x^2 − y^2 which is a saddle point.

Question: Is there a way to recognize if a critical point is a max a min or a saddle?

The answer to this question is a “partial” YES. We first have to define the Discriminant D:

Definition 1. Given a function z = f(x, y) we define

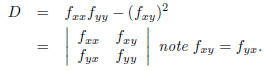
We have the following result:

Theorem 1. Assume that (x₀, y₀) is a critical point for the function z = f(x, y). Let D be the
discriminant above evaluated at (x₀, y₀). Then

1. if D < 0 -> the critical point is a saddle

2. if D > 0 (note f_xx = 0 impossible)

(a) and f_xx > 0 -> the critical point is a min

3. if D > 0

(a) and f_xx < 0 -> the critical point is a max

4. if D = 0 no info

Exercise 1. Consider first the function f(x, y) = x^2 − y^2. We already know that (0, 0) is a critical
point. We have: f_x = 2x, f_y = −2y and hence

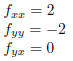
which implies D = −4 < 0 and (0, 0) is a saddle point:

On the other hand if f(x, y) = x^2 + y^2

we still get the same critical point (0, 0), but in this case

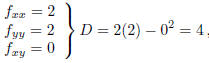
so max or min but f_xx = 2 > 0 so min.

We finally consider the function f(x, y) = x^4 + y^4

It is easy to check that again (0, 0) is a critical point, but now f_xx = 12x^2, f_yy= 12y^2 and f_xy = 0
and at the point (0, 0)

D = 0,

so there is no conclusion that we can make. We need to make a sort of “manual” inspection: since
for any point near zero we have

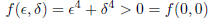
it follows that (0, 0) is a local min point.

Remark. A proof of the Second Derivative Test is rather involved. But there are two fundamental
steps in it : the quadratic approximation of a function near a point (otherwise called the Taylor
polynomial of degree 2) and the Second Derivative Test for quadratic functions. These two facts are
stated in the following lemmas:

Lemma 2. [ Quadratic Approximation of a Function of two variables ] Given a function
z = f(x, y) and a point P₀ = (x₀, y₀) we have the following second order approximation for f near
P₀:

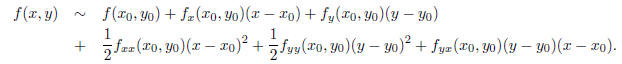
Lemma 3. [Second Derivative Test in a Special Case] Consider the quadratic function

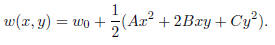
Clearly O = (0, 0) is a critical point. Then

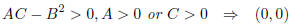	is a minimum point
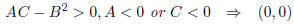	is a minimum point
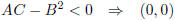	is a saddle point.

For the proof of this lemma see SD in Lecture Notes.

Remark. Notice that in Lemma 3

and hence D = AC −B^2. To prove the Second Derivative Test for arbitrary functions one first uses
Lemma 2 to approximate the function f(x, y) near the critical point by a quadratic function . Then
one uses Lemma 3.

4 Global max/min: Boundaries and Infinity

In this section we pass from considering local max/min to global ones. Let’s start with the following:
Exercise 2. Consider the function f(x, y) = x^2 + y^2 defined on the domain

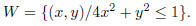
Compute global max and min of f on this domain.

Solution : We first observe that if the global max and min occur inside W then it must be also a
local max and min. We know from the previous example that there is no local max for f, but there
is a local min at (0, 0). This is also the global minimum since for any other point P = (x₀, y₀) one
has

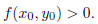
But what about the global max? For this we have to look at what happens to f at the boundary
(perimeter) of W, also denoted with @W. We have to evaluate f on this boundary and decide if f
has a max on it. Since the function and the domain W are symmetric with respect to the x−axis
we will only check the values of f on the upper boundary of W, let’s denote it :

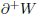It is easy to parametrize 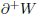by

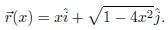
The value of f on 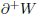is given by

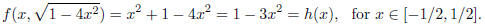
Now h(x) is a function of one variable and it is not difficult to show that on its domain its max
occurs at x = 0, which translate into the fact that f has two max on the boundary of W, more
precisely at P₊ = (0, 1) and P_- = (0,−1). We also have that

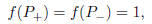
and this is the global max of f on W.

Question: What is the global max of f when we allow it to be defined on the whole plane?

Since there is no boundary we can evaluate f on points P = (x, y) “going to infinity”, that is such
that |x| or |y| . Clearly on these points the value of f = x^2 + y^2 will tend to infinity as
well, so the function does not admit a global max.

5 Level curves and level surfaces

You already have seen an example of level curves: any topographic map is made by drawing several
level curves relative to the 3D landscape that it represents. In fact if h(x, y) is the function that
represents the altitude at point P = (x, y), then the graph of this function is the landscape and the
topographic map is made by representing the (level ) curves that are obtained by considering all the
points at a certain altitude.

We have the following definition:

Definition 2. Given a two variable function z = f(x, y), for any scalar C we call the level curve
γC of f the set

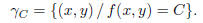
These level curves are represented on the xy−plane and their collection is called contour map:

Exercise 3. Consider the function f(x, y) = y − x^2. Draw the contour map of this function.

We have a similar definition for functions of three variables :

Definition 3. Given a three variable function w = f(x, y, z), for any scalar C we call the level
surface SC of f the set

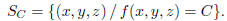
These level surfaces are represented on the xyz−space and their collection is also called contour
map.

Exercise 4. Consider the function f(x, y, z) = 4x^2 + y^2 + 9z^2. Draw the contour map of this
function.

Study Guide 1. Think about the following questions:

• Why in Theorem 1 I said that if D > 0 then it must be f_xx ≠ 0?

• Draw several contour maps and try to see how the picture looks like at max, min and saddle
point.