Numerical Linear Algebra

3.1 – Overview

Numerical linear algebra includes a class of problems which involves multiplying
vectors and matrices, solving linear equations , computing the inverse of a matrix, and
computing various matrix decompositions. It is one of the areas where knowledge of
appropriate numerical methods can lead to rather substantial speed improvements.

3.2 – Types of Matrices

In numerical linear algebra , efficient algorithms will take advantage of the special
structure of a matrix. In addition to the rectangular matrix, special matrix types include
symmetric matrices, symmetric positive definite matrices, band-diagonal matrices, block-diagonal
matrices, lower and upper triangular matrices, lower and upper band diagonal
matrices, Toeplitz matrices, and sparse matrices.

Each of these matrices is stored in a different way , generally in an array in
memory. A general matrix is usually stored as one row after another in memory. A
symmetric matrix can be stored in either packed or unpacked storage, and we may store
either the lower triangle, the upper triangle, or both. Suppose that n is the dimension of a
symmetric matrix. Unpacked storage requires n² locations in memory, while packed
storage requires n(n +1) / 2 units. In both cases, we typically store symmetric matrices
row after row. Lower and upper triangular matrices may also be stored in both packed
and unpacked form.

Figures 3.1 and 3.2 illustrate the storage of lower, upper, and symmetric matrices
in packed and unpacked storage. Bold number illustrate a location in memory that
contains an element of the matrix and non-bold elements contain a location in memory
which contains garbage. The advantage of packed storage is, of course, efficient use of
memory. The advantage of unpacked storage is that this storage usually allows for faster
computation. This occurs for a number of reasons, but one important reasons is that block
versions of common algorithms can be applied only if matrices are stored in unpacked
form.

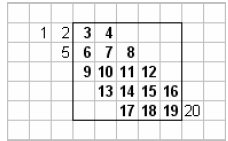
Band diagonal matrices are stored in a different fashion. Let 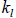denote the number
of lower bands, let 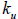denote the number of upper bands, and let 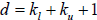. A band
diagonal matrix is stored in an nd element arrays. Each d units in the array correspond
to the nonzero elements of a row of A . For example, consider the following example of a
5x5 band diagonal matrix with 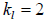and 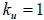. Figure 3.3 illustrates the storage of
such a matrix. The advantage of storing the matrix this way is both efficient use of
memory and computational speed.

Figure 3.1: Storage of Lower, Upper, and Symmetric Matrices
(Unpacked Storage)

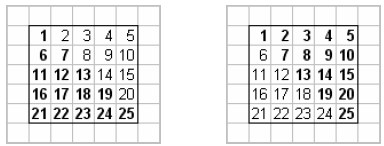
Figure 3.2: Storage of Lower, Upper, and Symmetric Matrices
(Packed Storage)

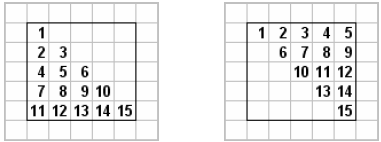
Figure 3.3: Storage of Band Matrix

A sparse matrix is a large matrix that contains few non- zero elements . Sparse
matrices are most often stored in compressed row format. Compressed row format
requires 3 arrays, which we label r , c , and v . The array v contains the values of all of
the nonzero elements in the matrix. The array c contains column in which each
corresponding nonzero element is located. The array r points to the location in c which
contains the elements that correspond to a row.

For example, consider the following sparse matrix,

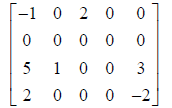
We could store this matrix as

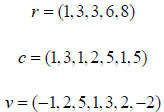
The final type of matrix (which is often useful in time-series econometrics
applications) is a Toeplitz matrix. A Toeplitz matrix has the form,

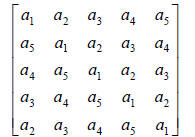
A Toeplitz matrix can be stored as, .

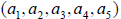3.3 – Elementary Linear Algebra and the BLAS

Elementary linear algebra operations include operations such as y← Ax ,
C ← A^T B , and y← L^-1x . Often, these operations can be implemented in a few lines of
code. There are, however, more efficient ways to implement these types of algorithms.
This differences most important in matrix-matrix computation (e.g. C ← A^T B ), but can
occasionally be useful in matrix-vector computations (e.g. y← Ax , y← L^-1x ).

The Basic Linear Algebra Subroutines (BLAS) contains efficient implementations
of these and many other algorithms. The BLAS are a set of FORTRAN subroutines, but
CBLAS ports these subroutines to C using an automatic converter called Fortran²C. In
order to apply the CBLAS, you must be relatively familiar with pointers. Consider
GEMM (which is the routine for multiplying two rectangular matrices). The routine
computes C ←α op(A)op(B) +β C , where op(A) = A or op(A) = A^T .



Notice that every variable here is a pointer. The variable transa determines where
op(A) = A or op(A) = A^T . The variables m and n are the dimensions of C . The variable
k is the number of columns or A , which is also equal to the number of rows in B . The
variables lda, ldb, and ldc, store the “leading dimension” of A , B , and C . This option
allows the algorithm to refer to the following types of matrices,

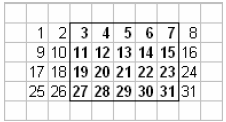
In this case, we have a 4 by 5 matrix, with a leading dimension of 8, starting at location 3.
Notice that this allows us the call the BLAS algorithms on sub-matrices without reallocating
memory.

BLAS is divided in to level-1, level-2, and level-3 algorithms. Level-1 algorithms
perform operations on vectors (and are O(n) ), level-2 algorithms operate on a vector and
a matrix (and are O(n² ) ), and level-3 algorithms operate on two matrices (and are
O(n³ ) ).