mental-math
Mental Math
Mental Math has several roles in elementary school.
For students, mental math can help
commit arithmetic facts to memory, but more importantly it
•solidifies understanding of place value and the
commutative , associative, and distributive
rules .
•teaches how numbers can be rearranged and
manipulated and how, often, the same answer
can be reached in several different ways .
These skills help prepare the student for algebra,
where the numbers are replaced by letters.
Properly presented, mental math can make this learning an enjoyable game.
Teachers must be adept at mental math because they
will be teaching it. More importantly,
a teacher's mental calculation skills need to be very good to figure out what
errors students are
making |- teachers must be able to verify answers quickly and mentally while
looking over a
student's shoulder, and must be able to quickly judge the correctness of
students' answers in
whole-class sessions.
Mental Math and calculators Being able to do
complicated computations in your head is not
one of the goals of mental math | that's what calculators are for. But with
calculators there is
no need to simplify calculations by rearranging numbers, so that skill is not
developed, leaving
the students without a necessary prerequisite for algebra.
In Math 201 you will get plenty of practice with
mental math. We will be working with numbers
somewhat larger than those that appear in elementary school. To understand the
strategies,
we need to practice on problems where the answer or even the technique is not
immediately clear.
Thus, for example, we will do problems like finding 19*21. Here are the basic
methods:
| Basic Methods | Example |
| Rearranging | 17 + (83 + 39) = (17 + 83) + 39 = 139 |
| Split numbers as sums or products 113*4 = 100*4 + 13*4 | 113*4 = 100*4 + 13*4 |
| `Compatible numbers': find pairs of numbers which are easily combined |
25*17*4 = (25*4)*17 = 1700 |
| `Compensation': adjusting the problem to an easier one with the same answer |
see below |
| Left-to-right may be easier | 3*721 = (3*700) + (3*21) |
| Methods for multiplying/dividing by 10, 4, 5, 8, 9, 25 | see below |
These methods can be applied in combination, and are
especially useful when combined with
estimation .
Rearranging means using the associative,
commutative, and distributive laws to simplify or to
`split o an easier problem'. Examples:
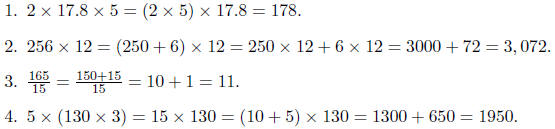
Compatible numbers are pairs of numbers which are
easily combined. For the problem 83 +
124 + 17 the numbers 83 and 17 are compatible, and for 4*23*20*25 the 4 and 25
are
compatible. For the problem 23*5, think of the compatible pair 20 and 5, so 23*5
= 20*5+15.
Compensation comes in four varieties.
| For +, one addend gives to the other | 97 + 156 = 100 + 153 | move 3 over |
| For -, both change by the same amount (try to round o the subtrahend) | 97-59 = 98-60 | +1 to both |
| For *, one factor gives to the other | 12*50 = 6*100 | move *2 over *2 to both |
For 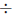 , each
number is multiplied by the same thing , each
number is multiplied by the same thing |
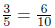 |
Mental Multiplication and Division Here are the ve most useful methods:
| If you want to | simply | Example |
| Multiply by 4 Divide by 4 |
double twice. halve twice. |
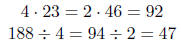 |
| Multiply by 5 Divide by 5 |
halve and multiply by 10. divide by 10 and double. |
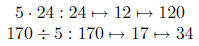 |
| Multiply by 9 | use 9x = 10x-x. | 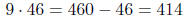 |
Once you have practiced these methods you can try their extension to factors of 8 and 25:
| Multiply/divide by 8 | double/ halve 3 times | 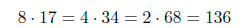 |
| Multiply by 25 | halve twice and multiply by 100 | 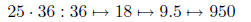 |
| Divide by 25 | remember each 100 is 4 25's | 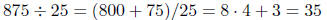 |
Amaze your friends! There is a wonderful trick based on the algebra fact
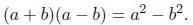
Notice that a is the average of the two numbers
being multiplied, and b is the difference from
the average . Thus to nd 19*21 one takes a = 20 (the average) and b = 1 (the
difference from
the average) to get 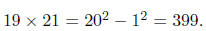 Another example:
Another example: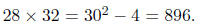
Try this for
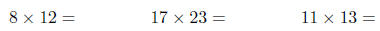
You can use this trick to quickly find almost all
products of numbers less that 20 provided you
know the squares of the numbers 11 - 20, namely 121; 144; 169; 196; 225; 256;
289; 324; 361; 400.
Example: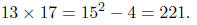
Estimation
Estimation is useful in two situations: (i) for
solving problems where only an approximate answer
is necessary, and (ii) as a check on the reasonableness of complex computations .
1. Example of (i): A car gets 31 miles a gallon.
About how far will it go on a full 12.8 gallon
gas tank? Solution by estimation :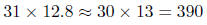 miles.
miles.
2. Example of (ii): We need to calculate
123.234*1.88976. By estimation this is 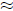 120*2
=
120*2
=
240. This can be used to check a calculator answer or to avoid using one.
Estimation is usually done by `rounding o ' numbers. The standard, familiar method is
Round fives up: to round to a certain place, tuncate
there if the next digit is less than 5,
truncate and take the next value up if the next digit is 5 or above. Example:
Rounding 1,245 to
the tens place gives 1,250, rounding it to the hundreds place gives 1200.
Several quicker ways of rounding are useful in estimation:
• Round to nice numbers as in
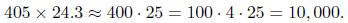
•Front end estimate| Truncate after the first one
or two digits, as in 1217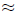 1200. This
1200. This
estimate is always low.
•Front end and adjust Truncate, then adjust for the
bit left out. Thus for 1257+647 we
can thnk 1200 + 600 = 1800, then adjust by 57 + 47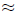 100
to get 1900.
100
to get 1900.
Sometimes it is important to avoid being too high or
low. One gets a high estimate by
consistently rounding up and a low estimate by consistently rounding down, where
\consistently"
means doing the same thing to each number in the calculation. Example: A car
gets 31 miles a
gallon. Is a full 12.8 gallon gas tank enough to get to a city 319 miles away?
Clearly we want to
estimate low. Do so on each factor: 31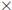 12.8 >
30
12.8 >
30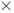 12 = 360, so there is enough gas.
12 = 360, so there is enough gas.
Range estimates. Find high and low estimates;
the answer is between. Example: 12.3234 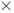
18.8976 is more than 12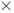 18 = 180 + 36 = 218
but less than 13
18 = 180 + 36 = 218
but less than 13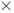 20 = 260.
20 = 260.
Skill at estimation is an essential prerequisite for
long division, and long division is the main
mathematical application of estimation.
| Prev | Next |