Math 181 Worksheet
Find the derivatives of the following functions.
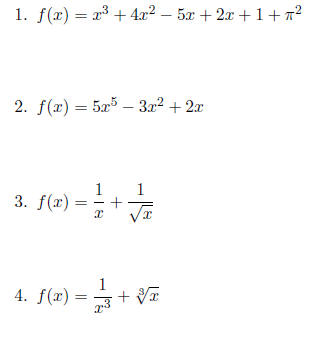
Use product rule on the following functions.
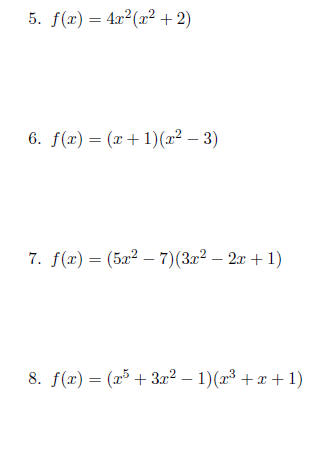
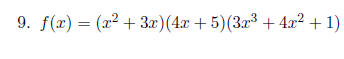
Use quotient rule on the following functions.
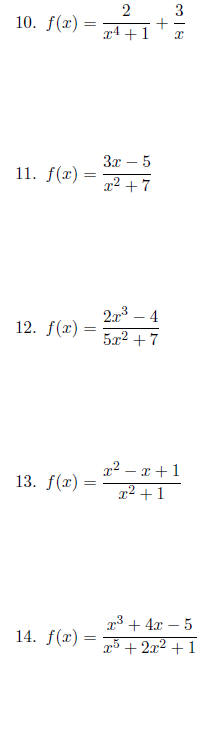
15. The area of a mold colony after t days after it starts t grow is given by A(t) = 4t2 − t − 1 cm2.
a) Find A'(t).
b) Find the instantaneous rate of change at day 1.
c) Find the slope of the line tangent to the mold colony curve where t = 2.
d) Find the equation of the line tangent to the mold colony curve where t = 2.
e) Find the instantaneous rate of change when the area of the mold colony is 32
cm2.
16. A population of bacteria grows so that t hours after
the start of the experiment at time t = 0,
the population is P(t) = 4t2 − 3t + 1 milligrams (mg).
a) Find P'(t). b) Find the instantaneous rate of change of
P at time t = 2.
c) Find the equation of the line tangent to the curve P(t) when t = 2.
d) Find dP/dt when t = 3.
e) Find the slope of the tangent line to the curve when P = 25 mg.
17. The mass of a bacterial colony in a beaker after t days is M(t) = 2t3 + 1 mg.
a) Find M'(t).
b) How fast is the population increasing after 1 day?
c) How fast is the population increasing after 2 days?
d) How fast is the population increasing after 3 days?
e) How fast is the population increasing after 10 days?
18. A person is being medicated. The concentration of a certain drug t hours after the start of treatment is given by
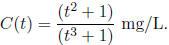
a) Find C'(t).
b) What is the rate of change in the concentration after half an hour?
c) What is the rate of change in the concentration after 1 hour?
d) Is the concentration increasing or decreasing after 1 hour?
19. Poiseuille’s law states that the velocity v of the blood in a small
artery with a circular cross
section of radius R is given by v(r) = A(R2
− r2) where r is the distance from the
center of
the artery and A is a constant. Find v'(r).
20. The distance traveled by a moving object at a time t is equal to
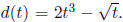Find the
instantaneous velocity: (a) at time t; (b) at the time t = 4.
21. A ball is thrown vertically upwards with an initial velocity of 60 ft/seec.
After t sec its height
above the ground is given by s = −16t2 +
60t. Find its instantaneous velocity after t sec.
What is so special about t = 15/8 ?
22. At the start of an experiment, a culture of bacteria is found to contain
10,000 bacterium. The
growth of the population was observed and was found that at any subsequent time
t (hours)
after the start of the experiment, the population size p(t) could be expressed
by the formula
p(t) = 2500(2 + t)2. Determine the formula
for the rate of growth of the population at any
time t, and in particular calculate the growth rate for t = 15 min and for t = 2
hr.
23. The proportion of seeds of a certain species of tree that scatter further
than distance r from
the base of the tree is given by
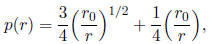
where r0 is a constant. Find the rate of change of the proportion with
respect to distance
and calculate p '(2r0).
24. When a bright light is directed toward the eye, the
pupil contracts. Suppose that the relationship
between R, the area of the pupil (in square millimeters ), and x, the brightness
of the
light source (in lumens), is given by
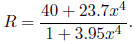
The rate of change dR/dx is called the sensitivity at
stimulus level x.
a) Find the formula for the sensitivity as a function of x.
b) Show that R decreases from 40 to 6 as x increases without bound.
25. During rapid changes in pressure , the pressure p and
density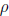 
of a gas vary according to the
law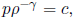 
where 
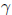and c are consants. Calculate 
.
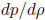26. According to the Schutz-Borisoff law, the amount y of
substrate transformed by an enzyme
in a time interval t is given by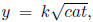 
where c is
the concentration of the enzyme,
a is the initial concentration of the substrate, and k is a constant. What is
the rate at
which the substrate is being transformed (assuming that the concentration of
enzyme remains
constant)?
27. Consider a sense organ which, when it receives a
stimulus, produces a number of action
potentials. Suppose at a particular time t sec from the start of stimulus, the
total number of
action potentials is given by
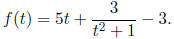
Find the rate of change of the number of action potentials at any time t.
28. The absolute temperature T of a gas is given by T =
cPV , where P is its pressure, V its
volume, and c is some constant depending on the mass of a gas. If P(t) = (t2
+ 1) and
V (t) = (2t + t-1)
as functions of time, find the rate of change of T with respect to time.
29. The density of algae in a water tank is equal to D =
n/V , where n is the number of algae and
V the volume of water in the tank. If n and V vary with time t according to the
formulas
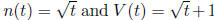, calculate the rate of change of the density
with respect to time.
30. A bacterial colony grows in a circular colony on a
Petri dish containing an agar gel with the
appropriate nutriment. The area A of the colony (in mm2) is a
quadratic function of the
number t of days since the start of the experiment, and it is known to have the
form
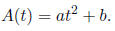
Students measure the area of the colony at the beginning
of different days since the start of
the experiment as follows:
At what rate is the area of the bacterial colony growing after (a) 3 days? (b) 6 days?
31. Some large birds cannot start flight on land, but
instead must begin flight by diving off a
cliff. A bird dives so that its height H (in feet) above the water below the
cliff at time t (in
seconds) after beginning the dive is given by the following date:
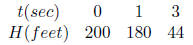
The height is given by a quadratic equation of the form
H(t) = at2 + bt + c.
What is the velocity of the bird after (a) 1 second? (b) 3 seconds?
| Prev | Next |