MATH 1450 Chapter 1 Review
1 Linear Equations
Tool: We can add, subtract, multiply and divide both sides of
an equation by the same quantity (except no division by
zero). So we can simplify equations to solve for variables.
If a=b , then (assuming no zeros in denominators )
a+ c=b+ c
a-c=b-c
a· c=b· c
a/c=b/c
1/a=1/b
Tool: Absolute value equations may be split into two linear
equations without absolute value bars . The equation
∣ax +b∣=k
means
ax+ b=k or ax+ b=-k
Tool: In word problems there is no recipe. Look at the
question to find the variable(s) you need. Put together with
any given (or implied) numbers and see if the equation makes
sense. Look at the different types of word problems in the
text to gain a feel for what’s out there.
2 Nonlinear equations
Tool: Group terms on one side of equation and factor. If
(x-r) (x-s)=0 , then x=r or x=s
Tool: Isolate square on one side and take square root of both
sides. The equation (ax+b)2=k is equivalent to the pair
of equations
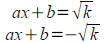
Tool: Completing the square (see p. 54 for alternate version).
Use for quadratic equations ax2+bx+c=0 too hard to
factor. Subtract c from both sides and divide through by a
to get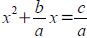 
. Then add
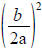to both sides and
factor to obtain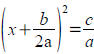 
, which you can square root .
Tool: Quadratic formula gives equivalent solution to
completing the square. Use when coefficients are nasty .
For ax2+bx+c=0 we have two solutions
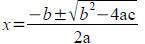
Basic Equation: (solve for s)
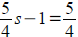
Rational Equation : (solve for r, check extraneous solution)
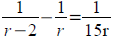
Formulas: (solve for h)
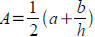
Absolute Value Equations: (solve for x)
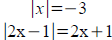
Linear Word problem:
A gambler plays the stock market. He bets $10000 spread
between a low risk stock returning 5% and a high risk stock
returning 10%. Assuming no crashes, total income for the
year is $850. How much did he invest in each stock?
Factor problem: (solve for w)
w=w2+12
Square root problem : (solve for y)
Recall that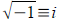 
.
(3y+4 )2+4=0
Completing the square problem: (solve for x)
x2-4x+5=0
Polynomial factoring : (solve for x, four solutions)
x4-16=0
Rational quadratic: (solve for v, check extraneous solution)
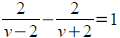
Quadratic formula problem : (solve for t)
1.21t2-3.54t+7.29=0
Ans: t=1.463±1.971i
Tool: Solving equations with roots you solve by
raising both
sides to the appropriate power and simplifying/solving.
Recall that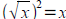 
and
.
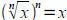Note that in some problems you may have to square both
sides more than once to remove the roots .
3 Inequalities
Tool: Just like for equations, we can add, subtract, multiply
and divide both sides of an inequality by the same quantity
(except no division by zero). The only catch is that if you
multiply or divide by a negative quantity, you must switch
the sign (this means no multiplying through by variables,
because you don't know if they are positive or negative ).
Tool: Absolute value inequalities may be transformed into
linear inequalities as follows . (It helps to think of absolute
value as denoting size or distance.) If ∣x∣< k , then x is no
larger than k in magnitude and -k < x< k .
Alternatively, if we switch to ∣x∣>k , then x lies outside
of a bounded interval, so x< -k or x>k .
Tool: Nonlinear inequalities that are factorable may use the
cut- point method (p. 68). In summary you look at each
factor and its zero on the number line. Decide whether each
zero is a solution. The zeros mark out intervals on the
number line. Pick a test point on the interior of each interval.
If the test point solves the inequality, mark the interval as part
of the solution.
| Prev | Next |