GRAPHING LINEAR EQUATIONS IN TWO VARIABLES

The graphs of linear equations in two variables are straight lines. Linear equations may be written in several forms:

Slope- Intercept Form : y = mx+ b

In an equation of the form y = mx + b, such as y = −2x − 3, the slope is m and the y-intercept is the point (0, b). To graph equations of this form, construct a table of values ( Method 1) or use the slope and y-intercept ( Method 3) (see Examples 1 and 6).

General Form: ax + by = c

To graph equations of this form, such as 3x − 2y = −6, find the x- and y-intercepts (Method 2), or solve the equation for y to write it in the form y = mx + b and construct a table of values (see Example 2).

Horizontal Lines: y = b

The graph of y = b is a horizontal line passing through the point (0, b) on the y-axis. To graph an equation of this form, such as y = 4, plot the point (0, b) on the y-axis and draw a horizontal line through it (see Example 4). If the equation is not in the form y = b, solve the equation for y.

Vertical Lines: x = a

The graph of x = a is a vertical line passing through the point (a, 0) on the x-axis. To graph a vertical line, such as 4x + 12 = 0, solve the equation for x to write it in the form x = a, plot the point (a, 0) on the x-axis, and draw a vertical line through it (see Example 5).

METHOD 1: CONSTRUCT A TABLE OF VALUES

To graph equations of the form y = mx and y = mx + b,

1) Choose three values for x. Substitute these values in the equation and solve to find the corresponding y-coordinates.
2) Plot the ordered pairs found in step 1.
3) Draw a straight line through the plotted points. If the points do not line up, a mistake has been made.

Example 1: Graph y = −2x − 3

To graph the equation, choose three values for x and list them in a table. (Hint: choose values that are easy to calculate, like −1, 0, and 1.) Substitute each value in the equation and simplify to find the corresponding y-coordinate. Plot the ordered pairs and draw a straight line through the points.

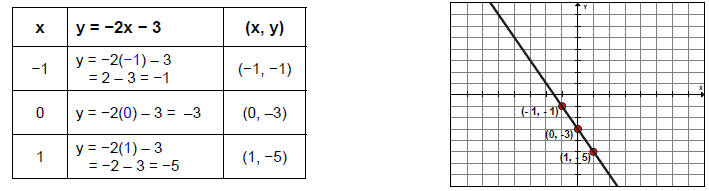
Example 2: Graph 3x − 2y = −6

The equation 3x − 2y = −6 is written in the general form. To graph this equation with a table of values, first solve the equation for y to write it in the form y = mx + b, as shown:

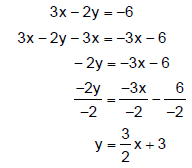
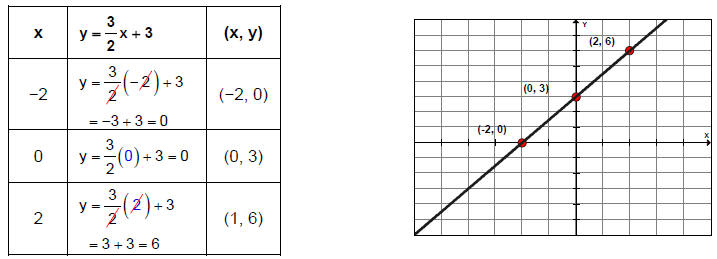
Next, choose three values for x and calculate the corresponding y- coordinates . (Hint: to cancel fractions, choose multiples of the denominator.) Plot the points in the table and draw a line through them.

METHOD 2: FIND THE X- AND Y-INTERCEPTS

In Example 2, the line crosses the x-axis at (−2, 0) and y-axis at (0, 3). The point where the line crosses the x-axis is called the x-intercept. At this point, the y-coordinate is 0 The point were the line crosses the y-axis is called the y-intercept. At this point, the x-coordinate is 0.

When an equation is written in the general form, such as −2x + 4y = 8, it is easier to graph the equation by finding the intercepts.

1) To find the x-intercept, let y = 0 then substitute 0 for y in the equation and solve for x.
2) To find the y-intercept, let x = 0 then substitute 0 for x in the equation and solve for y.
3) Plot the intercepts, label each point, and draw a straight line through these points.

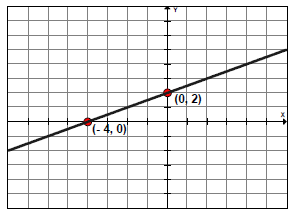
Example 3: Graph −2x + 4y = 8

1) To graph the equation, find the x- and y-intercepts.

To find the x-intercept, let y = 0 and solve the equation for x.

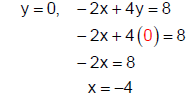
The x- intercept is (−4, 0).

To find the y-intercept, let x = 0 and solve the equation for y.

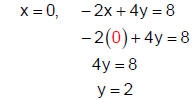
The y-intercept is (0, 2).

2) Next plot each intercept, label the points, and draw a line through them

Graphing Horizontal and Vertical Lines

The graph of y = b is a horizontal line passing through the point (0, b), the y-intercept. The graph of x = a is a vertical line passing through the point (a, 0), the x-intercept.

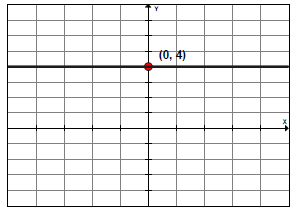
Example 4: Graph y = 4

To graph the equation, plot the intercept on the y-axis, label the point, and draw a horizontal line through the point.

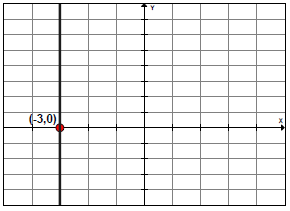
Example 5: Graph 4x + 12 = 0

First, solve the equation for x to write it in the form x = a.

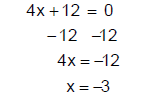
The x-intercept is (−3, 0). Plot this point on the x-axis, label the point, and draw a vertical line through the point.

METHOD 3: USE THE SLOPE AND Y-INTERCEPT

To graph an equation using the slope and y -intercept,

1) Write the equation in the form y = mx + b to find the slope m and the y-intercept (0, b).
2) Next, plot the y-intercept.
3) From the y-intercept, move up or down and left or right, depending on whether the slope is positive or negative . Draw a point, and from there, move up or down and left or right again to find a third point.
4) Draw a straight line through all three points.

Example 6: Graph 2x + 5y = 10.

To graph the equation using the slope and y-intercept, write the equation in the form y = mx + b to find the slope m and the y-intercept (0, b).

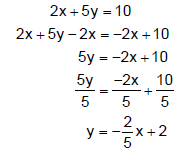
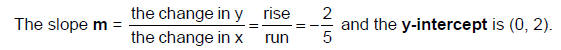
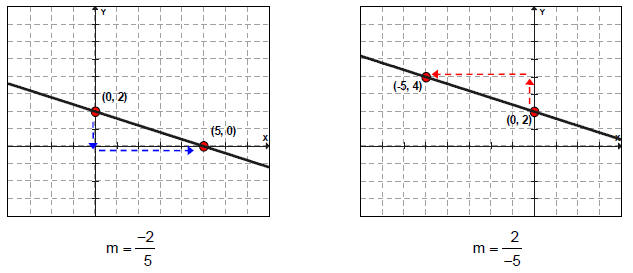
Now, plot the y-intercept. From there, move up or down two units (the rise) then move right or left five units to the right (the run) to find additional points.

When the slope is negative, make the change in y negative to locate points to the right of the y-intercept; make the change in x negative to locate points to the left of the y-intercept.