Arrays
1D Array Representation In Java, C, and C++
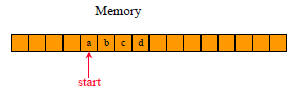
• 1-dimensional array x = [a, b, c, d]
• map into contiguous memory locations
Memory
• location(x[i]) = start + i
Space Overhead
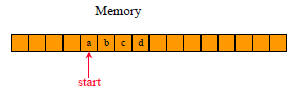
space overhead
= 4 bytes for start
+ 4 bytes for x.length
= 8 bytes
(excludes space needed for the elements of x)
2D Arrays
The elements of a 2-dimensional array a
declared as:
int [][]a = new int[3][4];
may be shown as a table
a[0][0] a[0][1] a[0][2] a[0][3]
a[1][0] a[1][1] a[1][2] a[1][3]
a[2][0] a[2][1] a[2][2] a[2][3]
Rows Of A 2D Array

Columns Of A 2D Array

2D Array Representation In Java, C, and C++
2-dimensional array x
a, b, c, d
e, f, g, h
i, j, k, l
view 2D array as a 1D array of rows
x = [row0, row1, row 2]
row 0 = [a, b, c, d]
row 1 = [e, f, g, h]
row 2 = [i, j, k, l]
and store as 4 1D arrays
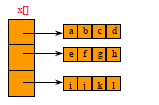
x. length = 3
x[0].length = x[1].length = x[2].length = 4
Space Overhead
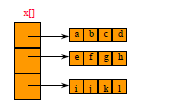
space overhead
= overhead for 4 1D arrays
= 4 * 8 bytes
= 32 bytes
= ( number of rows + 1) x 8 bytes
Array Representation In Java, C, and C++

• This representation is called the array-of-arrays
representation.
• Requires contiguous memory of size 3, 4, 4, and 4 for the
4 1D arrays.
• 1 memory block of size number of rows and number of
rows blocks of size number of columns
Row-Major Mapping
• Example 3 x 4 array:
a b c d
e f g h
i j k l
• Convert into 1D array y by collecting elements by rows.
• Within a row elements are collected from left to right.
• Rows are collected from top to bottom.
• We get y[] = {a, b, c, d, e, f, g, h, i, j, k, l}

Locating Element x[i][j]
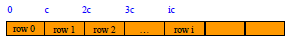
• assume x has r rows and c columns
• each row has c elements
• i rows to the left of row i
• so ic elements to the left of x[i][0]
• so x[i][j] is mapped to position
ic + j of the 1D array
Space Overhead

4 bytes for start of 1D array +
4 bytes for length of 1D array +
4 bytes for c (number of columns)
= 12 bytes
(number of rows = length /c)
Disadvantage
Need contiguous memory of size rc.
Column-Major Mapping
a b c d
e f g h
i j k l
• Convert into 1D array y by collecting elements
by columns.
• Within a column elements are collected from
top to bottom.
• Columns are collected from left to right.
• We get y = {a, e, i, b, f, j, c, g, k, d, h, l}
Matrix
Table of values. Has rows and columns, but
numbering begins at 1 rather than 0.
a b c d
 row
1
row
1
e f g h
 row
2
row
2
i j k l
 row
3
row
3
• Use notation x(i,j) rather than x[i][j].
• May use a 2D array to represent a matrix.
Shortcomings Of Using A 2D
Array For A Matrix
• Indexes are off by 1.
• Java arrays do not support matrix operations
such as add , transpose, multiply , and so on.
– Suppose that x and y are 2D arrays. Can’t do x + y,
x –y, x * y, etc. in Java.
• Develop a class Matrix for object-oriented
support of all matrix operations . See text.
Diagonal Matrix
An n x n matrix in which all nonzero
terms are on the diagonal .
Diagonal Matrix
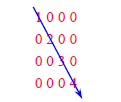
• x(i,j) is on diagonal iff i = j
• number of diagonal elements in an
n x n matrix is n
• non diagonal elements are zero
• store diagonal only vs n2 whole
Lower Triangular Matrix
An n x n matrix in which all nonzero terms are either
on or below the diagonal.
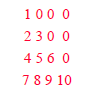
• x(i,j) is part of lower triangle iff i >= j.
• number of elements in lower triangle is 1 + 2 +
… + n = n(n+1)/2.
• store only the lower triangle
Array Of Arrays Representation
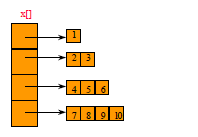
Use an irregular 2-D array … length of rows is not
required to be the same.
Creating And Using An Irregular Array
// declare a two -dimensional array variable
// and allocate the desired number of rows
int [][] irregularArray = new int [numberOfRows][];
// now allocate space for the elements in each row
for (int i = 0; i < numberOfRows; i++)
irregularArray[i] = new int [size[i]];
// use the array like any regular array
irregularArray[2][3] = 5;
irregularArray[4][6] = irregularArray[2][3] + 2;
irregularArray[1][1] += 3;
Map Lower Triangular Array Into A 1D Array
Use row-major order, but omit terms that are
not part of the lower triangle.
For the matrix
1 0 0 0
2 3 0 0
4 5 6 0
7 8 9 10
we get
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Index Of Element [i][j]

• Order is: row 1, row 2, row 3, …
• Row i is preceded by rows 1, 2, …, i-1
• Size of row i is i.
• Number of elements that precede row i is
1 + 2 + 3 + … + i-1 = i(i-1)/2
• So element (i,j) is at position i(i-1)/2 + j -1 of
the 1D array.
| Prev | Next |